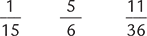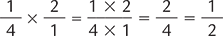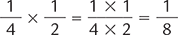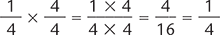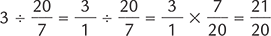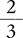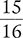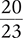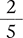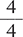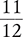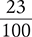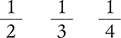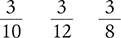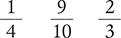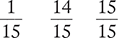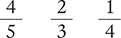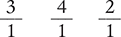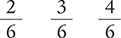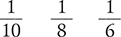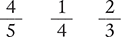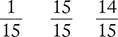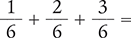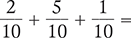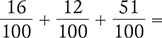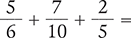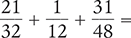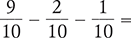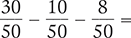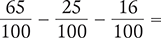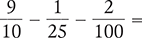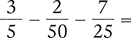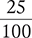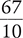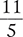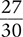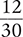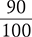1.2 Fractions
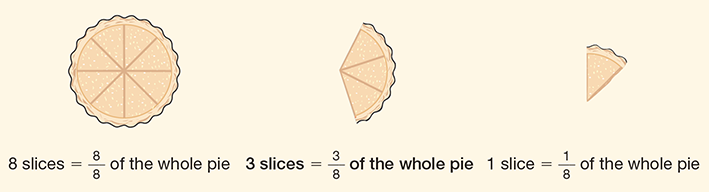
When an object is divided into parts, each part is a fraction of the whole. For example, a pie might be divided into eight equal slices, each of which is a fraction, or ⅛, of the whole pie. The pie is still whole but has been divided into eight slices. If you select one slice, it is one-eighth of the whole pie, or 1 (the number of slices in the selection) over 8 (the number of slices in the whole pie). In the fraction ⅜, the selection is 3 of the 8 slices (see Figure 1.1).
Figure 1.1 Fractions of a Whole Pie
A common fraction consists of a numerator (top number) and a denominator (bottom number). For example, in the fraction ⅛, the numerator represents the number of pieces that are selected from the pie (1 piece), and the denominator represents the total number of pieces in the pie (8 pieces).
Quick Study
The orientation of the numerator and the denominator in a fraction can be remembered with this catchphrase: The denominator is down below the line in a fraction.
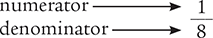
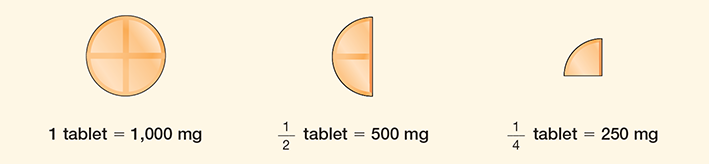
Just as a pie can be divided into parts, so can a tablet. Splitting a scored tablet is a common procedure for both pharmacy personnel and patients. Figure 1.2 shows how splitting a 1,000 milligram (mg) tablet into smaller parts relates to fractions.
Figure 1.2 Fractions of a Tablet
A fraction with the same numerator and denominator has a value of 1.
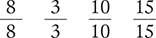
A fraction with a value less than 1 (numerator less than denominator) is called a proper fraction.
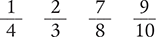
A fraction with a value greater than or equal to 1 (numerator greater than or equal to denominator) is called an improper fraction.
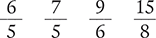
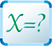Math Morsel
Proper fractions always have a value less than 1, or less than the “whole” of the pie, tablet, or other object.
The combination of a whole number and a fraction is called a mixed number. A mixed number can be converted into an improper fraction by multiplying the whole number by the denominator and adding the numerator.
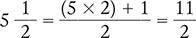
An improper fraction can be converted into a mixed number by dividing the numerator by the denominator. The whole number is maintained, and the remainder becomes the new numerator (which is placed over the original denominator).
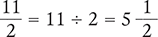
A fraction in which the numerator, the denominator, or both the numerator and the denominator contain a fraction is called a complex fraction.
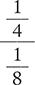
Two fractions that appear different but have the same value are called equivalent fractions. The following examples are equivalent fractions: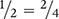 
and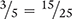 
. Two fractions are equivalent (equal) only if the product of the numerator (a) of the first fraction and the denominator (d) of the second fraction are equal to the product of the denominator (b) of the first fraction and the numerator (c) of the second fraction.
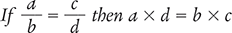
Consider the fractions ¾ and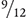 
. These fractions are equal if 3 × 12 = 4 × 9. When you multiply the numbers, you see that 3 × 12 = 36 and 4 × 9 = 36. Therefore, ¾ and 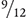are equivalent or proportional fractions. The concept and relationship of equivalent fractions and proportions are important principles in pharmacy calculations.
Comparing Fractions
When comparing fractions with the same numerator, the fraction with the smaller denominator has the larger value.
Math Morsel
The symbol > means “is greater than,” and the symbol < means “is less than.”
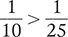
If two fractions have the same denominator, the fraction with the larger numerator has the larger value.
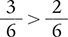
Example 1.2.1
Which nitroglycerin tablet is the smallest dose?
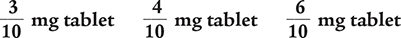
Answer: The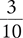 
mg tablet is the smallest dose.
Example 1.2.2
Which nitroglycerin tablet is the largest dose?
Answer: The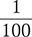 
grain tablet is the largest dose.
If two fractions have different numerators and denominators, you must thoughtfully assess their values. This assessment can be performed by converting the fractions to equivalent fractions with the same denominator and then comparing the two fractions. This method is described in detail in the next pages. When medications are dosed using fractions, it is important to recognize which strengths are largest and smallest.
Adding and Subtracting Fractions
Addition and subtraction are commonly used mathematical operations in pharmacy practice. A sum is the result of adding two or more numbers together. A difference is the result of subtracting two or more numbers. As a pharmacy technician, you may find yourself calculating the sum or difference of both whole numbers and fractions.
Safety Alert
When working with fractions, pharmacy technicians should always include the units (if known) after the number—for example, a ½ mg tablet. Without clearly marked units, serious medication errors can occur.
When adding or subtracting fractions with unlike denominators, it is necessary to create a common denominator, or a number into which each of the unlike denominators can be divided evenly. Think of it as making both fractions into “pieces of pies” with equal slices. Creating a common denominator requires transforming each fraction by multiplying it by a fraction that is equal to 1.
Multiplying a number by 1 does not change the value of the number (5 × 1 = 5). Therefore, if you multiply a fraction by a fraction that equals 1 (such as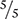 
), you do not change the value of the fraction. This mathematical rule allows for the conversions in the following examples.
Example 1.2.3
Find the sum of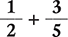 
.
The lowest number that can be divided evenly by both 2 and 5 is 10. A quick way to determine a possible common denominator is to multiply the denominators (2 × 5 = 10). Thus, 10 will be the common denominator for the two fractions, and each fraction must be converted to tenths.
To convert 
to tenths, multiply by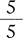 
. The product is 
.
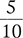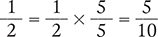
To convert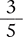 
to tenths, multipl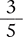y by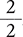 
. The product is 
.
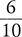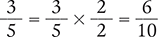
Then ad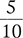d and 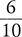and convert the sum into a mixed number.
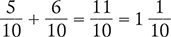
Answer: The sum of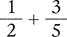 
is 
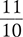or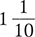 
.
Example 1.2.4
Find the sum of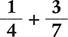 
.
A possible common denominator is 28 because 4 × 7 = 28.
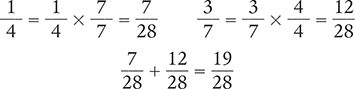
Answer: The sum of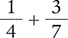 
is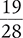 
.
Sometimes, multiplying the denominators is not an efficient way for finding a common denominator. When there are three or more fractions, follow the steps in Table 1.3.
Table 1.3 Steps for Finding a Common Denominator
Step 1. Find the prime number* factors for each denominator.
15 = 3 × 5 6 = 2 × 3 36 = 2 × 2 × 3 × 3 |
||||||||
Step 2. Determine the quantity of prime number factors for each denominator.
|
||||||||
Step 3. For each prime number factor in column 2 of the table above, take the highest of these counts.
|
||||||||
Step 4. The least common denominator is the product of the individual prime number factors multiplied by the count, as listed in Step 3. 2 × 2 × 3 × 3 × 5 = 180 |
||||||||
*A prime number is a number that is divisible only by 1 and itself (such as 2, 3, 5, 7, etc.). |
Once two fractions have been converted to fractions
with a common denominator, the numerators can be added together. After the numerators have been added, it may be necessary to reduce the resulting fraction. Typically, fractions should be reduced to their lowest terms at the end of a calculation. This process of reducing fractions to their lowest terms requires cancellation, or the crossing out of common factors or like terms in both the numerators and the denominators. Once the largest number possible has been canceled out of the numerator and the denominator, the fraction is simplified or reduced to its lowest terms. For example, consider the fraction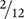 
. This fraction can be simplified or reduced to its lowest terms.
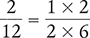
The common factor in the numerator and in the denominator is the number 2. You can cancel the number 2 from the numerator and the denominator, as shown below.
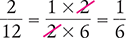
After cancellation, the fraction ⅙ remains.
Example 1.2.5
Reduce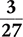 
to its lowest terms.
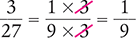
Another way to reduce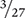 
to its lowest terms is to divide both the numerator and the denominator by a common factor (in this case, 3).
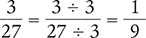
Answer: The lowest terms of the fraction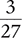 
is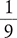 
.
Example 1.2.6
Reduce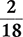 
to its lowest terms.
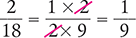
Another way to reduce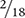 
to its lowest terms is to divide both the numerator and the denominator by a common factor (in this case, 2).
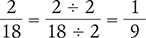
Answer: The lowest terms of the fraction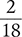 
is .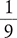
When adding or subtracting fractions that have the same denominator, add or subtract the numerators and place the number over the common denominator. It may be necessary to reduce the answer if it is not in its lowest terms.
Example 1.2.7
Find the difference of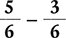 
.
Because these fractions have a common denominator of 6, subtract the numerators and place the difference over the common denominator.
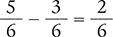
Then reduce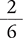 
to its lowest terms.
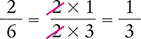
Answer: The difference of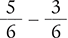 
is 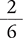, reduced to 
.
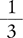When subtracting fractions that have different denominators, find a common denominator and convert to equivalent fractions. Then subtract the numerators and place the number over the common denominator. It may be necessary to reduce the answer to its lowest terms.
Example 1.2.8
Find the difference of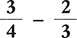 
.
To begin, find the least common denominator (in this case, 12). To convert to equivalent fractions, multiply ¾ by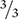 
and ⅔ by 
.
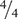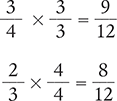
Then replace the original fractions with the equivalent fractions, subtract the numerators, and place the difference over the common denominator.
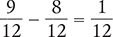
Answer: The difference of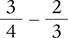 
is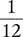 
.
When adding or subtracting a mixed fraction, first convert the mixed fraction to an improper fraction. Then, if necessary, find the common denominator and convert to equivalent fractions. Last, add or subtract the numerators and place the number over the common denominator. It may be necessary to reduce the answer to its lowest terms.
Example 1.2.9
Find the difference of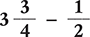 
.
To begin, change the mixed number to an improper fraction.
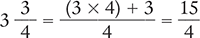
Then replace the mixed number with the improper fraction in the original problem.
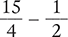
Because the second fraction (½) has a denominator of 2, this fraction must be changed to a fraction that has a denominator of 4. To do this, multiply the numerator and denominator of ½ by 2.
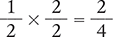
Next, replace the second fraction with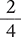 
.
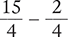
Then subtract the numerators and place the difference over the common denominator.
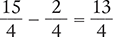
Finally, change the improper fraction to a mixed number by dividing 13 by 4.
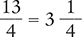
Answer: The difference of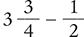 
is 
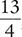, or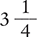 
.
Math Morsel
A mixed number has a whole number in front of a fraction.
Example 1.2.10
Find the difference of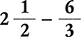 
.
To begin, change the mixed number to an improper fraction.
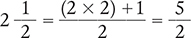
Then replace the mixed number in the original problem with the improper fraction.
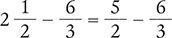
Next, find the least common denominator (in this case, 6). Convert to equivalent fractions.
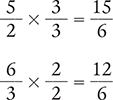
Then replace the original fractions with the equivalent fractions, subtract the numerators, and place the difference over the common denominator.
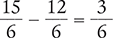
Finally, reduce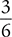 
to its lowest terms.
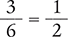
Answer: The difference of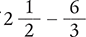 
is 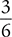, reduced to .
Multiplying and Dividing Fractions
In pharmacy practice, you may need to multiply fractions prior to filling a prescription or a medication order. For example, you may have to determine the number of tablets a patient will need to last for a certain period. When you multiply fractions together, you multiply numerators by numerators and denominators by denominators. The result, called a product, is then reduced to its lowest terms (see Table 1.4).
Table 1.4 Guidelines for Multiplying Fractions
|
|
|
Consider this example of two proper fractions being multiplied.
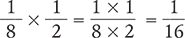
When more than two fractions are multiplied, all the numerators are multiplied by one another and all the denominators are multiplied by one another.
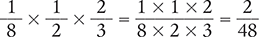
The product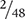 
can be reduced to 
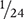. Alternatively, the 2 in the numerator and the 2 in the denominator could have been canceled out prior to multiplication.
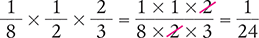
When a whole number is multiplied by a fraction, rewrite the whole number as a fraction. In the following example, the whole number (in this case, 5) is rewritten as a fraction with a denominator of 1 or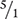 
.
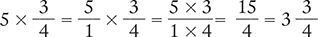
Example 1.2.11
Find the product of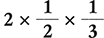 
. Then reduce the product to its lowest terms.
To begin, rewrite the whole number as a fraction.
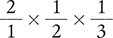
Next, multiply all the numerators together and all of the denominators together.
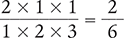
Finally, reduce the fraction 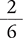to its lowest terms.
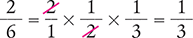
Answer: The product of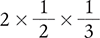 
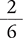is , reduced to .
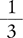Math Morsel
A whole number can be written as an improper fraction in order to multiply fractions.
In pharmacy practice, you may also need to divide fractions to find the quotient. To divide fractions, you change the division sign (÷) to a multiplication sign (×) and invert the number (create a reciprocal) to the right of the multiplication sign. Then you multiply the numerators together and the denominators together and reduce the answer to its lowest terms. You can use this same method if only the numerator is a fraction or if only the denominator is a fraction (see Table 1.5).
Table 1.5 Guidelines for Dividing Fractions
|
|
Consider this example of two proper fractions being divided.
You begin by changing the division sign to a multiplication sign. Then you create the reciprocal of the fraction to the right of the multiplication sign. The reciprocal of ⅓ is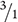 
.
Then you multiply the fractions by multiplying the numerators and the denominators.
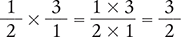
The quotient is an improper fraction and should be reduced to its lowest terms, which is a mixed fraction.
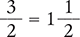
Example 1.2.12
Find the quotient of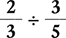 
.
To begin, change the division sign to a multiplication sign and create the reciprocal of the fraction to the right of the multiplication sign.
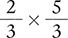
Next, multiply the numerators and the denominators of the fractions.
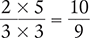
Finally, reduce the improper fraction to its lowest terms, which is a mixed number.
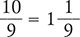
Answer: The quotient of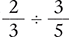 
is 
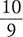, reduced to 
.
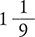Using Dimensional Analysis to Multiply and Divide Fractions
Dimensional analysis is a problem-solving method that uses the math principle that any number can be multiplied by 1 without changing its value. For that reason, this method is often used in the multiplication and division of fractions. (Refer to Chapter 4 for further instruction on the use of dimensional analysis.)
Name Exchange
Dimensional analysis is also known as the factor label method or the unit factor method.
To understand dimensional analysis, you must first understand equivalent fractions.
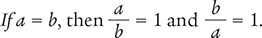
Therefore, any equality (a = b) can form two fractions (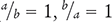
).
This principle allows you to solve problems by setting them up as fractions that are multiplied by other fractions. You must set up the problems so that the starting units cancel out one another and, consequently, you are left with the desired units.
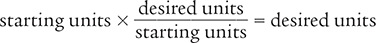
For example, you can use the dimensional analysis format above to calculate the number of minutes in one hour. The starting units (the units you are given) are hours, and the desired units (the units you want to find) are minutes. The starting units of hours are canceled out and leave the desired units as minutes.
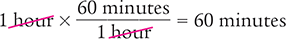
Consider calculating the number of minutes in one day. There are 24 hours in one day and 60 minutes in one hour. The desired units are minutes per day (minutes/day). Set up fractions to solve for minutes/day by canceling out the hour units.
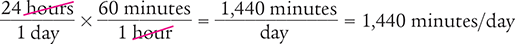
You can use this method to solve more complex calculations. Consider calculating the number of seconds in one day. There are 60 seconds in one minute, 60 minutes in one hour, and 24 hours in one day. The desired units are seconds per day (seconds/day), and the units that must be canceled out are minutes and hours.
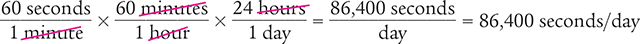
Dimensional analysis is useful in performing many types of pharmacy calculations. For example, dimensional analysis may be useful when partial doses, such as 1/2 tablet or 3/4 teaspoonful, are prescribed. The following example demonstrates this calculation.
Example 1.2.13
How many milligrams are in ½ of a furosemide tablet shown in the label?
You can solve this problem using either the dimensional analysis method or the division method.
Dimensional Analysis Method
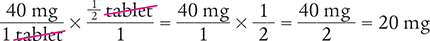
Division Method
Alternatively, you can divide the strength of the tablet (40 mg) by 2 because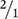 
is the reciprocal (or inverse) of ½.
40 mg ÷ 2 = 20 mg
Answer: For this medication label, there are 20 mg in ½ of a furosemide tablet.
1.2 Problem Set
Indicate which number is the numerator in the following fractions.
Indicate which number is the denominator in the following fractions.
Circle the fraction with the highest value.
Circle the fraction with the lowest value.
Find the sum of the following fractions.
Find the difference of the following fractions.
Reduce the following fractions to their lowest terms and rewrite the fractions as mixed numbers if necessary.
Applications
A patient has taken ¼ tablet, ½ tablet, 1½ tablets, and ¾ tablet. In total, how many tablets has the patient taken?
Which dose contains the largest amount of medication: one tablet containing
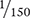grain or two tablets containing 
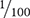grain in each tablet?You are to measure ¼ grain of medication into individual containers. Your bulk container holds 375 grains. How many individual containers can be prepared from one bulk container?
Table sugar is needed for making simple syrup. The first formula calls for ½ pound (lb) of sugar to make enough syrup; the second formula requires ⅘ lb of sugar; the third formula requires ¼ lb of sugar; and the fourth formula requires 2½ lb of sugar. You need to use all four formulas to create one batch of simple syrup.
How many bags of sugar must be purchased if it is packaged in 2 lb bags?
How many bags of sugar must be purchased if it is packaged in 5 lb bags?
Self-check your work in Appendix A.