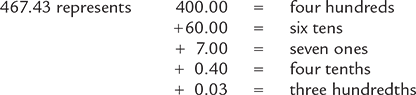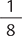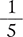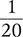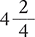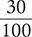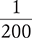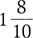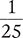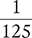1.3 Decimals

An understanding of the decimal system is crucial to pharmacy calculations because most medication orders are written in decimals. The decimal system is based on the Arabic number system that you learned earlier in this chapter. In the decimal system, 10 Arabic numbers are used: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The placement of these numbers in a decimal is important to the interpretation of the decimal.

A decimal is an Arabic number that has two components: a zero or a whole number component (which has a value of 1 or greater) and a fractional component (which has a value of less than 1, or parts of a whole). These two components are separated by a decimal point.

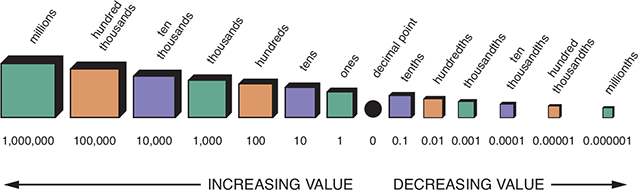
The position or placement of each digit in a decimal determines its place value. The position of each digit to the left of the decimal point signals a tenfold increase in its value, and the position of each digit to the right of the decimal point signals a tenfold decrease in its value. Figure 1.3 illustrates the relative place value of each digit in a decimal. Memorize these place values so that you can correctly write and read decimals.

Figure 1.3 Decimal Units and Values

Writing Decimals

You can write any fraction as a decimal. When writing a decimal, you place the whole number component to the left of the decimal point, and the fractional component to the right of the decimal point. To determine the fractional component, divide the numerator by the denominator. For example, the fraction 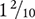can be written as the decimal 1.2. Inversely, you can write any decimal as a fraction. For example, the decimal 2.33 can be written as the fraction .

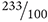When you are writing a decimal and there is no whole number component, you must place a zero to the left of the decimal point. This zero is called a leading zero. Healthcare personnel must consistently use leading zeros in the practice setting because their placement helps to avoid medication errors from the misinterpretation of decimals.

Table 1.6 provides guidelines on how to interpret decimals and determine their values. As you can see by the examples, decimal values are determined by the place values of their digits.

Reading Decimals

A decimal is read from left to right. First, you read the whole number component to the left of the decimal point. Then you say “and” or “point” to refer to the decimal point. Finally, you read the fractional component to the right of the decimal point. For example, the decimal 2.375 is read as “two point three seven five” or “two and three hundred seventy-five thousandths.”

Table 1.7 provides a summary of interpreting decimals. The table reveals how to express fractions as decimals as well as how to read the decimals.

Adding and Subtracting Decimals

When adding or subtracting decimals, place the numbers in columns so that the decimal points are aligned vertically. You may need to add zeros after the decimal point to correctly align the decimal points. Add or subtract from the far-right column to the far-left column.

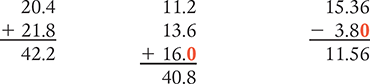
Multiplying and Dividing Decimals

Unlike adding and subtracting decimals, the multiplication of decimals does not require you to align the decimal points. You simply multiply decimals the same way that you multiply whole numbers. However, you will omit the decimal places until the last step of the calculation. When you arrive at your answer, you then add the total number of decimal places that are in the two numbers being multiplied (which is the number of decimal places in your answer), count that number of places from right to left in the answer, and insert a decimal point.

To divide decimals, change both the divisor (the number you are dividing by) and the dividend (the number being divided) to whole numbers by moving their decimal points the same number of places to the right. If the divisor and the dividend have a different number of digits after the decimal point, choose the one that has more digits and move its decimal point a sufficient number of places to make it a whole number. Then move the decimal point in the other number the same number of places, adding a zero at the end if necessary.

In the first example below, the divisor (3.625) has more digits after the decimal point than the dividend (1.45). Therefore, you would move the divisor’s decimal point three places to the right to make it a whole number. You would then move the decimal point in the dividend the same number of places and add a zero at the end (as shown below). In the second example below, the dividend (1.617) has more digits after the decimal point than the divisor (2.31). Therefore, you would move the dividend’s decimal point three places to the right to make it a whole number. You would then move the decimal point in the divisor three places to the right and add a zero at the end (as shown below).

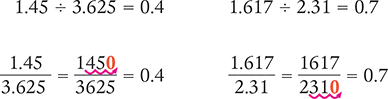
Rounding Decimals

Rounding is the process of replacing a number by another number of approximately the same value but with fewer digits. Rounding numbers is essential in pharmacy calculations and, in the rounding examples in this textbook, is performed as the last step in the calculations process. The purpose of rounding is to keep the numbers that you are working with to a manageable size. It is important to recognize, however, that rounding will affect the accuracy to which a medication can be measured. In some cases, it may be appropriate to calculate a dose to the nearest whole milliliter and, in other cases, to round to the nearest tenth or hundredth of a milliliter. Depending on the medication and strength prescribed, it may not be possible to accurately measure a very small quantity such as a hundredth of a milliliter.

When numbers with decimals are used to calculate a volumetric (volume-related) dose, a number with multiple digits beyond the decimal often results. It is not practical to retain all of these digits, as a dose cannot be accurately measured beyond the hundredths or thousandths place for most medications. Most commonly, a volumetric dose is rounded to the nearest tenth. For doses that are measured in weight, it is common practice to round to the hundredths or thousandths place, or as precisely as the particular measuring device (or medication) will permit.

To round an answer to the nearest tenth, carry the calculation out two places or to the hundredths place. If the digit in the hundredths place is 5 or greater, add 1 to the tenths place number. If the digit in the hundredths place is less than 5, round the number down by omitting the digit in the hundredths place.

5.65 becomes 5.7               4.24 becomes 4.2

The same procedure may be used when rounding to the nearest hundredths place or thousandths place.

The following example shows how an exact dose can be rounded to the nearest tenths, hundredths, and thousandths place.

WORKPLACE WISDOM

In most cases, a zero occurring at the end of a string of digits after the decimal point is not written. This zero is called a trailing zero. An exception to this rule may occur when rounding results in a zero as the last place value. When the last digit resulting from rounding is a zero, there are cases in which this zero should be written because it is considered significant to that particular problem or dosage. In such cases, the amount can be measured out to an exact zero as the place value.

1.3 Problem Set

Write the following decimals.

1. seven hundred eighty-four and thirty-six hundredths

2. nine tenths

Express the following fractions in decimal form.

In each group of decimals, circle the decimal with the highest value.

12. 3.1   1.7   4.1

13. 0.5   0.56   0.6

In each group of decimals, circle the decimal with the lowest value.

14. 2.02   2.12   2.1

15. 0.16   0.167   0.017

Identify the digit in the designated place value of the number below.

92,375.046

16. tenths place

17. thousandths place

18. hundredths place

State the place value of the underlined digit.

19. 18,240.6

20. 7.2391

21. 621.508

22. 0.98

23. 40. 023

Find the sum of the following decimals.

24. 0.34 + 1.54 =

25. 1.39 + 1.339 =

Find the difference of the following decimals.

26. 15.36 − 0.987 =

27. 3.09875 − 0.00045 =

28. 12.901 − 0.903 =

Find the product of the following decimals and round to the nearest hundredth.

29. 21.62 × 21.62 =

30. 0.9 × 500 =

Find the quotient of the following decimals and round to the nearest thousandth.

31. 12 ÷ 6.5 =

32. 0.8 ÷ 0.6 =

Round the following decimals to the nearest hundredth.

33. 3.872

34. 0.138

35. 0.076

Round the following decimals to the nearest thousandth.

36. 0.1961

37. 0.0488

Find the product of the following decimals and round to the nearest tenth.

38. 6.7 × 5.21 =

39. 0.45 × 3.1 =

Applications

40. Using the prescription below, answer the following questions. Note: The abbreviation po means “by mouth,” and the abbreviation TID means “three times a day.”

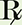    Alprazolam 0.25 mg

    

    Dosing instructions: 3 tablets po TID

    Quantity to dispense: 100 tablets

    1. How many milligrams is the patient taking with each dose?

    2. How many milligrams is the patient taking each day?

    3. How many tablets will the patient need for 14 days?

    4. Is the prescription written for enough tablets to last the patient until the next office visit in two weeks?

    5. The pharmacy plans to charge $7.59 plus the cost of the medication. The available products include the following:

       alprazolam 0.25 mg 100 tablets/$14.95

       alprazolam 0.5 mg 100 tablets/$17.46

       alprazolam 1 mg 100 tablets/$23.87

       Select the appropriate product and calculate the price for the patient. Based on the prescription provided, the pharmacy can dispense only 100 tablets.

41. The physician changes the prescription at the patient’s next visit. The new prescription is shown below. Note: The abbreviation po means “by mouth,” and the abbreviation TID means “three times a day.”

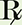    Alprazolam 0.25 mg

    

    Dosing instructions: 4 tablets po TID

    Quantity to dispense: 175 tablets

    The available products include the following:

    alprazolam 0.25 mg 100 tablets/$14.95

    alprazolam 0.5 mg 100 tablets/$17.46

    alprazolam 1 mg 100 tablets/$23.87

    1. How many milligrams is each dose?

    2. How much would 125 tablets of alprazolam 0.5 mg cost the pharmacy?

    3. How much would 50 tablets of alprazolam 1 mg cost the pharmacy?

    4. How many days would 50 tablets of alprazolam 1 mg taken TID last?

42. Sterile water is available in a 1 liter (L) container. You need to pour out 120 milliliter (mL) bottles for each patient.

    1. How many 120 mL bottles will you get from a 1 L bottle? (1 L = 1,000 mL)

    2. How many milliliters will be left over?

43. How many total milliliters need to be dispensed for the following prescription? Round your answer to the nearest whole milliliter. Note: The abbreviation mg means “milligrams”; the abbreviation mL means “milliliters”; and the abbreviation BID means “twice a day.”

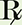    Augmentin 125 mg/5 mL suspension

    

    8.5 mL BID days 1–2

    5.75 mL BID days 3–7

44. Round the following amounts to the nearest whole dollar.

    1. $46.92

    2. 12 @ $1.26

    3. $7.37 ÷ 2 =

45. Calculate the following dollar amounts and round to the nearest cent.

    1. $5.84 × 12 =

    2. $0.415 × 269 =

46. Find the quotient and round your answer to the nearest hundredth.

    1. 34 ÷ 38 =

    2. 51 ÷ 60 =

    3. 83 ÷ 90 =

Self-check your work in Appendix A.