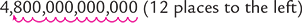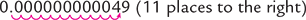1.4 Scientific Notation, Significant Figures, and Measurement Accuracy
Precision and accuracy are extremely important when performing pharmacy calculations. To maintain precision and accuracy, you should be aware of three important concepts: scientific notation, significant figures, and measurement accuracy.
Expressing Numbers in Scientific Notation
Standard notation is when a numeral is completely written out using Arabic numbers. An example of a number written in standard notation is 0.624 or 624. There are times when expressing a number in standard notation is inconvenient. It is not practical to write out numbers that have a large number of zeros (such as 5,200,000,000,000) or very small numbers (such as 0.00000025) in standard notation because of space issues as well as readability. In these cases, scientific notation may be utilized. Scientific notation is a method used to write numbers that have very large or very small numerical values.
 Math Morsel
Math Morsel
Exponents can be positive (102) or negative (10–2). The positive exponent 102 = 100, and the negative exponent 10−2 = 0.01.
To change a number written in standard notation to scientific notation, you can rewrite the number as a group of significant figures multiplied by 10 with an exponent. Significant figures are all the digits of a number that signify accuracy. An exponent is a number placed above and to the right of another number to show that it has been raised to a power. The number in the exponent indicates how many places the decimal has been moved, and the sign of the exponent (positive or negative) indicates the direction the decimal was moved. A positive exponent indicates a number greater than 1, and a negative exponent indicates a number less than 1.
Consider the following examples that use scientific notation.
6.24 × 1017 5.19 × 10−84
In the first example, the group of significant figures is 6.24, and the exponent is 17. Because 17 is a positive number, it is considered a positive exponent. In the second example, the group of significant figures is 5.19, and the exponent is −84. Because −84 is a negative number, it is considered a negative exponent.
Table 1.8 shows examples of values written in standard notation and their equivalence in scientific notation.
Table 1.8 Standard Notation and Scientific Notation Equivalence
Standard Notation |
Decimal Place Movement |
Scientific Notation |
|---|---|---|
6,500 |
|
6.5 × 103 |
120,000 |
|
1.2 × 105 |
921,000,000 |
|
9.21 × 108 |
4,800,000,000,000 |
|
4.8 × 1012 |
0.109 |
|
1.09 × 10–1 |
0.000587 |
|
5.87 × 10–4 |
0.00000026 |
|
2.6 × 10–7 |
0.000000000049 |
|
4.9 × 10–11 |
Counting Significant Figures
As mentioned earlier, significant figures are the digits of a number, often a measurement, that contribute to the degree of accuracy of the value. The number of significant figures is equal to the number of digits that are known with some degree of confidence plus the last digit (which is an estimate). The last digit is known as the lowest known place value. The lowest known place value is approximate because of many sources of error (including limitations of the measuring instrument, temperature variation, and the need to round at a certain point to make the number practical for calculations). For example, consider the number 8.16. There are three significant figures in this number (8, 1, and 6). The lowest known place value in 8.16 is 6.
In pharmacy practice, there are rules that determine how significant figures are counted. These rules are outlined in Table 1.9.
Table 1.9 Rules for Counting Significant Figures
Rule 1. Begin counting at the first nonzero digit. Rule 2. Continue counting to the right until you reach the place value that is last (or rounded). Rule 3. Count zeros that are located between digits as significant. Rule 4. Do not count zeros that are placed to the left of the first digit. These zeros only mark the place of the decimal. Rule 5. Recognize that one or more trailing zeros may or may not be significant, depending on the accuracy to which the number is held. |
 Safety Alert
Safety Alert
Pharmacy technicians should not use a trailing zero unless it is a significant figure that determines the accuracy of a number.
Consider the number 0.01023. You begin counting significant figures at the first nonzero digit. For this example, you would begin counting the significant figures at the first 1.
0.01023
Next, you continue counting to the right until you reach the lowest known place value. In this example, the lowest known place value is 3.
0.01023
Zeros that are located between digits are significant figures and should be counted. In this example, the zero between the 1 and 2 should be counted.
0.01023
Do not count zeros that are placed to the left of the first digit. These zeros are considered place markers. In this example, the zeros that precede 1 are not counted.
0.01023
Therefore, based on these rules, the number 0.01023 has four significant figures.
0.01023
Table 1.10 shows several numerals and their number of significant figures.
Table 1.10 Counting Significant Figures
Numeral |
Number of Significant Figures |
|---|---|
|
1.8 |
2 |
18.3 |
3 |
183 |
3 |
1.832 |
4 |
1,832 |
4 |
0.183 |
3 (not the leading zero) |
0.108 |
3 (not the leading zero) |
0.0108 |
3 (not the leading zero or the zero before the first digit) |
0.01 |
1 (not the leading zero or the zero before the first digit) |
0.8 |
1 (not the leading zero) |
8 |
1 |
10 |
2 |
Determining Measurement Accuracy
Accuracy is the degree to which a measurement matches the actual value of the quantity being measured. The degree of accuracy may be expressed as the number of significant figures or as a percent. A measurement with two-figure accuracy measures a value to within 5% of the actual value. Likewise, a measurement with three-figure accuracy measures a value to within 0.5% of the actual value. Accuracy range is the extent (upper and lower limits) that a value can be measured (see Table 1.11).
TABLE 1.11 Significant Figures and Degree of Accuracy
Number of Significant Figures |
Degree of Accuracy |
Accuracy Range for 100 mg |
|---|---|---|
2 |
within 5% |
95–105 mg |
3 |
within 0.5% |
99.5–100.5 mg |
4 |
within 0.05% |
99.95–100.05 mg |
5 |
within 0.005% |
99.995–100.005 mg |
When the degree of accuracy is known to a certain place value, the significant figures are counted only to that place value. Knowing the level of accuracy is important when considering the weighing capacity and sensitivity of a scale or balance in the pharmacy. More significant figures indicate a greater accuracy of known values.
Numbers greater than 100 have significant figures based on the relative accuracy of the measurement. If a number greater than 100 is accurate to the nearest 10, the zero in the ones place is considered an estimate and not significant. Only the digits to the left of that place value are considered significant. Significant figures are counted similarly for numbers that are accurate to the nearest 100 or larger. For example, if the following numbers are accurate to the nearest 10, they will have the indicated number of significant figures.
200 has two significant figures
1,800 has three significant figures
30,000 has four significant figures
Similarly, if the following numbers are accurate to the nearest 100, they will have the indicated number of significant figures.
200 has one significant figure
1,800 has two significant figures
30,000 has three significant figures
When multiplying or dividing, the answer should have the same number of significant figures as the original inexact number that has the fewest significant figures.
Example 1.4.1
An item is weighed on a balance with a degree of accuracy to the nearest tenth when measuring milligrams. The balance indicates that the item weighs 1.459 mg. How many significant figures does this weight have? What would the rounded value be?
Answer: Because the accuracy of the scale can be relied on only to the tenths place, the number of significant figures is two. The “5” and the “9” in the item’s weight are not considered significant figures because of the sensitivity of the scale being used. The weight should be rounded to 1.5 mg.
Example 1.4.2
Determine the product of 6.75 × 3 using the appropriate number of significant figures for accuracy.
Note the number of significant figures and the level of accuracy for each number: 6.75 has three significant figures and is accurate to the tenths place, whereas 3 has one significant figure and is accurate to the ones place.
Now, determine the actual product of the two numbers.
6.75 × 3 = 20.25
Answer: The product of 6.75 × 3 is 20.25. Because 3 has one significant figure, the product needs to be rounded to the tens place: 20.
Example 1.4.3
Determine the product of 12.59 × 1,572 using the appropriate number of significant figures for accuracy.
When you multiply two numbers together, the answer should have the same number of significant figures as the number that has the lesser number of significant figures in the equation. In this example, both numbers have four significant figures.
Now, determine the actual product of the two numbers.
12.59 × 1,572 = 19,791.48
Answer: The product of 12.59 × 1,572 is 19,791.48. Because both numbers in the problem have four significant figures, the answer can have only four significant figures: 19,790.
Using Exact Numbers
In pharmacy applications, it is typical to consider certain values as exact numbers. Exact numbers can be thought of as having infinitely many significant figures. The number of items is considered an exact number in pharmacy practice. For example, the number of tablets or the number of days are considered exact numbers. Consequently, you count only the significant figures in the measured (inexact) quantities, such as dosages.
1.4 Problem Set
Write the following numbers using standard notation.
6.8 × 104
1.87 × 106
1.03 × 107
8.4 × 10−4
7.68 × 10−3
6.239 × 10−5
Write the following numbers using scientific notation.
0.00000000329
390,000,000,000
0.0038
52,000,000,000,000,000
3,779,000
0.000000000202
Identify the number of significant figures in the following numbers. Assume that all final zeros in numbers without decimals are not significant.Note: The abbreviation mL means “milliliters”; the abbreviation mg means “milligrams”; the abbreviation mcg means “micrograms”; and the abbreviation kg means “kilograms.”
15.4324 grains
1,500 mL
0.21 mg
$1.07
100,000 mcg
507.2 mg
1.01 kg
0.001 mg
21,204.075 mcg
100 mL
Round the following numbers to three significant figures.
42.75
10.091
0.04268
18.426
0.003918
Round the following numbers to the hundredths place and state how many significant figures each number has.
0.3479
0.056921
1.9947
0.00986
1.0277
Calculate the following products and retain the correct number of significant figures in the answers.
0.67 × 95.2 =
1.26 × 24 =
325 × 0.5 =
Applications
You are to prepare capsules that contain 0.125 gram (g) of a drug. You have four partial containers of medication, which weigh 3.2 g, 1.784 g, 2.46 g, and 5.87 g. Assume that you have weighed each of the four containers with the same scale, and the accuracy is known to the hundredth gram.
Which amount will need to be rounded?
Which amount is not as accurate as it should be?
What amount of medication will be left over after making as many 0.125 g capsules as possible?
A unit dose of an oral medication requires 21.65 mg. You are to prepare 45 doses.
How many milligrams will you need?
How many significant figures does this amount have?
Self-check your work in Appendix A.