1.5 Estimates
Estimation is the process of finding an approximate solution or answer, known as an estimate, to a mathematical problem prior to performing the actual calculation. Determining an estimate allows you to verify whether your calculated solution is reasonable. Estimation can be used in both simple mathematical equations and more-complicated algebraic equations. This method may also be used in everyday tasks, such as rounding to the nearest whole dollar while shopping.
There are no set mathematical rules for estimation; however, it is commonly performed by rounding to the nearest whole unit that makes sense for the numbers involved. This whole unit may be the ones place, tens place, hundreds place, or even larger.
Estimating Sums and Differences
When estimating sums and differences, it is common practice to round the numbers to the nearest tens place, hundreds place, or thousands place, and then to add or subtract the rounded numbers. When rounding and then adding or subtracting, the values in the ones place and lower are often ignored. The following calculations compare an actual sum or difference with a corresponding estimate.

Estimation is a process that becomes easier with practice. A short list of numbers will often generate a fairly accurate estimate, whereas a longer list of numbers may require more practice and may be less accurate. The sum or difference determined by estimation cannot be relied on for accuracy when filling prescriptions or medication orders.
 Safety Alert
Safety Alert
Estimation can be used to double-check doses but should never be relied on for accuracy.
Estimating Products and Quotients
One commonly used method to estimate products or quotients is to round each of the original numbers. If any of the rounded numbers have zeros at the end of the numbers, you can temporarily drop the zeros before performing multiplication or division. Then the rounded numbers can be quickly multiplied or divided. In the case of multiplication, the appropriate number of zeros can be added to the answer. In the case of division, the number of zeros dropped from the divisor can be subtracted from the number of zeros dropped from the dividend. The following examples walk you through these steps.
Example 1.5.1
Estimate the product of 325 × 618. Then compare the estimated product to the actual product.
To begin, round the two numbers: 325 is closer to 300 than 400 and should be rounded to 300; 618 is closer to 600 than 700 and should be rounded to 600.
Next, temporarily drop the zeros from both values. You will replace these zeros once you arrive at the estimated answer.
300 becomes 3
600 becomes 6
Then multiply the rounded numbers.
3 × 6 = 18
Next, replace the appropriate number of zeros in the answer. Two zeros should be added for 300, and two zeros should be added for 600. As a result, you will add four zeros to 18.
180,000
Finally, calculate the actual product of 325 × 618.
Answer: The estimated product of 325 × 618 is 180,000; the actual product of this problem is 200,850.
Example 1.5.2
Estimate the product of 843 × 41. Then compare the estimated product to the actual product.
To begin, round the two numbers: 843 should be rounded to 800, and 41 should be rounded to 40.
Next, you can temporarily drop the zeros from both values. You will replace these zeros once you arrive at the estimated answer.
800 becomes 8
40 becomes 4
Then multiply the rounded numbers.
8 × 4 = 32
Next, replace the appropriate number of zeros in the answer. Two zeros should be added for 800, and one zero should be added for 40. As a result, a total of three zeros should be added.
32,000
Finally, calculate the actual product of 843 × 41.
Answer: The estimated product of 843 × 41 is 32,000; the actual product of this problem is 34,563.
Example 1.5.3
Estimate the quotient of 953 ÷ 52. Then compare the estimated quotient to the actual quotient.
To begin, round the two numbers: 953 should be rounded to 1,000, and 52 should be rounded to 50.
Next, temporarily drop the zeros from both values. You will replace these zeros once you arrive at the estimated answer.
1,000 becomes 10
50 becomes 5
Then divide the rounded numbers.
10 ÷ 5 = 2
Next, replace the appropriate number of zeros in the answer. To do so, subtract the number of zeros dropped from the divisor (in this case, one zero) from the number of zeros dropped from the dividend (in this case, two zeros). As a result, a total of one zero should be added to the estimated answer.
20
Finally, calculate the actual quotient of 953 ÷ 52.
Answer: The estimated quotient of 953 ÷ 52 is 20; the actual quotient of this problem is 18.3.
Example 1.5.4
Estimate the quotient of 5,355 ÷ 4.79. Then compare the estimated quotient to the actual quotient.
To begin, round the two numbers: 5,355 is closer to 5,000 than 6,000 and should be rounded to 5,000; 4.79 is closer to 5 than 4 and should be rounded to 5.
Next, temporarily drop the zeros, as necessary. You will replace these zeros once you arrive at the estimated answer.
5,000 becomes 5
5 remains 5
Then divide the rounded numbers.
5 ÷ 5 = 1
Next, subtract the number of zeros dropped from the divisor (in this case, no zeros) from the number of zeros dropped from the dividend (in this case, three zeros). As a result, a total of three zeros should be added to the estimated answer.
1,000
Finally, calculate the actual quotient of 5,355 ÷ 4.79.
Answer: The estimated quotient of 5,355 ÷ 4.79 is 1,000; the actual quotient of this problem is 1,117.95.
Example 1.5.5
A patient needs to take 3.75 mL of an oral liquid medication daily for 30 days. Estimate the total number of milliliters needed to fill this order. Then compare your estimated number of milliliters to the actual number. Finally, determine which bottle you will need to fill this order: a 120 mL bottle or a 180 mL bottle.
To begin, round 3.75 mL to 4 mL.
Next, multiply 4 mL by the number of days needed (30 days).
4 mL × 30 days = 120 mL
Finally, use the actual number (3.75 mL) in your calculation.
3.75 mL × 30 days = 112.5 mL
Answer: The estimated product of 4 mL × 30 days is 120 mL; the actual product of this problem is 112.5 mL. For that reason, you will select the 120 mL bottle to dispense 112.5 mL of this medication.
Estimating a Drug Dose
Estimating a drug dose before calculating the actual dose is helpful because the estimate can be used to double-check the accuracy of the actual dose. If the actual dose is not close to the estimated dose, then the calculations should be rechecked. When estimating a drug dose, the first step is to round the dose to a number you can easily divide by the available drug strength. Next, divide the rounded number by the available drug strength.
 Math Morsel
Math Morsel
Estimation can help to prevent dispensing errors by providing an approximation of the amount of product to dispense. Significant differences in the estimated and actual amounts should prompt pharmacy technicians to double-check their work for accuracy.
Example 1.5.6
An order for 12.5 mg of a drug needs to be filled. The pharmacy has 5 mg tablets in stock. Estimate the number of tablets needed for this dose and compare this estimated number to the actual number of tablets needed.
Because the order is for 12.5 mg of the drug, the dose to be measured out will be larger than one 5 mg tablet.
To begin, simplify the estimation by rounding down 12.5 mg to 10 mg. This rounding will make it easier to use the available dose to estimate the required number of tablets.
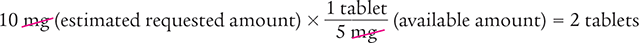
Now calculate the number of tablets needed for a 12.5 mg dose.
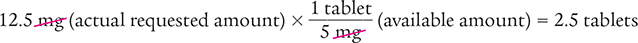
The calculated actual dose of 2.5 tablets can then be checked by comparing it with the estimated dose. In this case, the estimated dose was 2 tablets. Because the two tablet doses are similar, you can be more confident in the accuracy of your calculated dose.
Answer: The estimated number of tablets needed for 12.5 mg of this drug is 2 tablets, and the actual number of tablets needed is 2.5 or 2½ tablets.
In addition to drug doses, the volume to be dispensed and the size of the container needed can be useful estimates when preparing a drug for dispensing. For example, when dispensing a liquid medication, it is important to round up and overestimate the amount of liquid your patient will need. This action ensures that the individual receives enough medication.
Example 1.5.7
The pharmacy receives an order for a 10 days’ supply of a liquid antibiotic to be taken in a dose of 8.5 mL of medication three times a day. The pharmacy has 100 mL, 200 mL, and 300 mL bottles of this antibiotic in stock. Which size bottle of antibiotic should be dispensed?
To begin, round the dose: 8.5 mL/dose to 10 mL/dose. Recall that it is important to round up to make sure the patient has enough medication.
Then use this rounded value (estimated dose) to calculate the amount of medication needed per day. To do so, multiply the estimated dose by the number of doses each day.
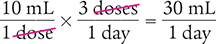
Consequently, the patient will need about 30 mL of the medication per day.
Because the patient needs to take this medication for 10 days, multiply the amount of medication per day by the number of days of therapy.
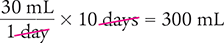
Now, determine the actual amount the patient will need for a 10 days’ supply.
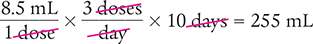
Therefore, the patient will need about 300 mL of the medication. The actual amount needed is 255 mL.
Answer: Because the patient will need 255 mL of medication, the 300 mL bottle is necessary to fill the prescription.
1.5 Problem Set
Round dollar amounts to the nearest whole dollar to find the estimated value. Then calculate the actual value.
$12.53 − $6.15 =
$6.28 + $1.99 + $3.98 =
$40 − $34.81 =
$100 − $18.29 =
$100 − $17.52 − $31.90 =
Round the two numbers and multiply them to find the estimated product. Then calculate the actual product.
6.8 × 7,656 =
4.02 × 350.07 =
598.4 × 0.015 =
4,569 × 0.0972 =
6,183 × 18 =
1,253 × 9.1 =
Round the two numbers and divide them to find the estimated quotient. Then calculate the actual quotient.
185 ÷ 18 =
18,015 ÷ 56 =
584.0 ÷ 8 =
844.23 ÷ 4.4 =
123 ÷ 14 =
Applications
Use rounding and estimation to solve the following problems.
A compounding pharmacy requires last-minute supplies. If the following items are needed, estimate how much the total cost will be.
food dye
$1.89
sugar, 2 bags
$4.25/bag
baking soda
$0.79
cherry flavoring
$2.39
bleach, 1 gal
$1.97
distilled water, 4 gal
$0.89/gal
Estimate how much sterile water for injection (SWFI) you will need for the following reconstitutions: 3.2 mL, 7.6 mL, 1.6 mL, and 4.1 mL. Choose from the following available vials (15 mL SWFI, 30 mL SWFI, and 50 mL SWFI).
A patient is receiving the following fluids: intravenous (IV) fluids, 1,723 mL; juice, 150 mL; and coffee, 126 mL. Estimate the patient’s intake to the nearest 10 mL.
A patient’s parenteral fluid intake for the first 24 hours after hospital admission includes the following: 780 mL normal saline (NS), three 50 mL piggybacks, 250 mL NS, three 1,000 mL bags of NS. Estimate the total to the nearest 100 mL amount.
Self-check your work in Appendix A.