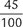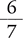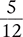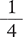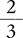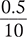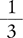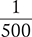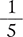2.2 Percents
The word percent means “per 100” or “hundredths.” Consequently, a percent expresses the number of parts compared with a total of 100 parts. A percent is represented by the symbol % and can be written as a ratio, a fraction, or a decimal. For example, 30% can be written as a ratio (30:100), a fraction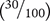 
, or a decimal (0.30). All three forms indicate 30 parts in a total of 100 parts.
Put Down Roots
The word percent comes from the Latin term per centum meaning “by the hundred.” Therefore, percent literally means “per 100.”
A percent can be visualized by comparing a stack of 100 pennies (equivalent to one dollar) next to smaller stacks of pennies (see Figure 2.2). A stack of 40 pennies equals 40% of one dollar, which can also be expressed as 40:100 or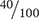 
or 0.40. Similarly, a stack of 5 pennies equals 5% of one dollar, which can also be expressed as 5:100 or 
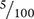or 0.05.
Figure 2.2 Comparison of Percents
Percents are often used to describe the strengths or concentrations of intravenous (IV) solutions and topically applied medications. The higher the percentage of dissolved substances in a solution or in a topical medication, the greater the strength. Both examples below may be expressed as 1:100,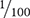 
, or 0.01.
Math Morsel
The higher the percentage of a dissolved substance, the greater the strength.
A 1% solution contains 1 g of medication per 100 mL of fluid.
A 1% hydrocortisone cream contains 1 g of hydrocortisone per 100 g of cream.
When performing calculations with medications described by percents, it is helpful to rewrite the medication as a fraction or ratio first. Then the ratio may be manipulated by multiplying or dividing both parts of the ratio by the same factor. As mentioned earlier, if the dose needs to be increased, you multiply the ratio by a factor. If the dose needs to be decreased, you divide the ratio by a factor.
Example 2.2.1
A 5% solution contains 5 g of solute per 100 mL of solution. If a patient is to receive 200 mL of solution, how many grams of solute will it contain?
You can either set up a ratio to solve this problem, or you can use the dimensional analysis method.
Ratio Method
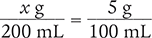
Because these fractions are equivalent, you can cross multiply and the equations will still equal one another.
x g (100 mL) = 5 g (200 mL)
Then solve for x by dividing each side of the equation by 100 mL and canceling the similar units (like units) in the numerators and in the denominators.
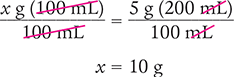
Dimensional Analysis Method
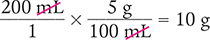
Answer: The 200 mL solution contains 10 g of solute.
Example 2.2.2
A 2% solution contains 2 g of solute per 100 mL of solution. How many milliliters of this solution are needed to give a dose of 6 g of solute?
You can either set up a ratio to solve this problem, or you can use the dimensional analysis method.
Ratio Method
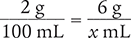
Because these fractions are equivalent, you can cross multiply and the equations will still equal one another.
x mL (2 g) = 100 mL (6 g)
Then solve for x by dividing each side of the equation by 2 g and canceling the similar units (like units) in the numerators and in the denominators.
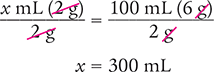
Dimensional Analysis Method
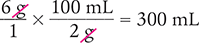
Answer: A 300 mL solution is needed to give a dose of 6 g of solute.x
Example 2.2.3
The medication label shows a 1% solution of Xylocaine. Write the percent as a fraction. Then determine the number of milligrams per milliliter (mg/mL) in a 1% solution of Xylocaine.
A 1% solution of Xylocaine contains 1 g of Xylocaine per 100 mL of solution.
To begin, write the percent as a fraction.
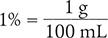
Then convert the fraction from grams per 100 mL to milligrams per 100 mL.
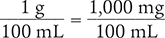
Finally, divide to solve the problem.
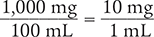
Answer: A 1% Xylocaine solution contains 10 mg/mL of medication.
When working in a pharmacy, you will need to know equivalent values for different mathematical expressions such as percents, fractions, ratios, and decimals. The examples shown in Table 2.1 show these equivalent mathematical expressions.
Table 2.1 Equivalent Mathematical Expressions
Percent |
Fraction |
Ratio |
Fraction |
|---|---|---|---|
45% |
|
45:100 |
0.45 |
0.5% |
|
0.5:100 |
0.005 |
Converting a Fraction to a Percent
Fractions compare a number of parts (the numerator) with a total number of parts (the denominator). This comparison is similar to a percent, in which the number of parts is compared with a total of 100 parts. There are two methods you can use to convert a fraction to a percent. One method is to convert the fraction to an equivalent fraction with a denominator of 100.
Consider the fraction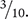 
.
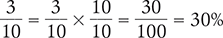
Another way to convert a fraction to a percent is to divide the numerator by the denominator, multiply by 100, and add a percent sign.
Consider the fraction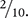 
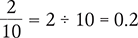
0.2 × 100 = 20%
Example 2.2.4
Convert the fraction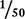 
to a percent.
You can solve this problem using two different methods: by making an equivalent fraction with a denominator of 100 or by dividing the numerator by the denominator, multiplying by 100, and adding a percent sign.
Making an Equivalent Fraction with a Denominator of 100
To begin, convert the fraction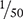 
to an equivalent fraction with a denominator of 100.
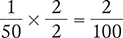
Then rewrite the fraction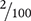 
as a percent.
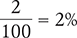
Dividing, Multiplying by 100, and Adding a Percent Sign
To begin, divide the numerator (1) by the denominator (50).
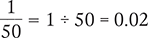
Next, multiply by 100, and add a percent sign.
0.02 × 100 = 2%
Answer: The fraction 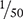is the same as 2%.
Converting a Ratio to a Percent
Recall that percent is the number of parts compared with a total of 100 parts. To convert the ratio 5:1 to a percent, you need to rewrite the ratio as a fraction (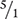
), and then convert the fraction to an equivalent fraction with a denominator of 100. In this case, you must multiply the numerator and denominator by 100 to create a fraction with a denominator of 100.
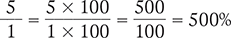
Another way to convert a ratio to a percent is to rewrite the ratio as a fraction; then multiply by 100; and, finally, add a percent sign.
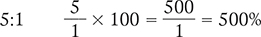
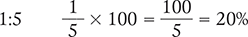
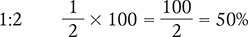
Example 2.2.5
A prescriber ordered a 1:1,000 solution. You have a 1% solution, a 0.5% solution, and a 0.1% solution in stock. Which one of these solutions will fill the order?
You can solve this problem using two different methods: by making an equivalent fraction with a denominator of 100 or by multiplying by 100, dividing, and adding a percent sign.
Making an Equivalent Fraction with a Denominator of 100
To begin, rewrite the ratio 1:1,000 as a fraction.
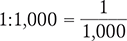
Note that the denominator of the fraction is 1,000. To determine the percent solution,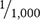 
needs to be rewritten as an equivalent fraction with a denominator of 100. To do this, divide both the numerator (1) and the denominator (1,000) by 10.
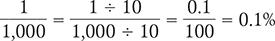
Multiplying by 100, Dividing, and Adding a Percent Sign
To begin, rewrite the ratio 1:1,000 as a fraction.
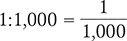
Next, multiply the fraction by 100.
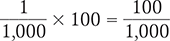
Finally, divide the fraction and add a percent sign to your answer.
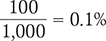
Answer: The 0.1% solution is the same concentration as the ordered 1:1,000 solution.
Converting a Percent to a Ratio
To convert a percent to a ratio, rewrite the percent as a fraction with a denominator of 100. Then reduce the fraction to its lowest terms. Finally, express this fraction as a ratio by making the numerator the first number of the ratio and the denominator the second number of the ratio.
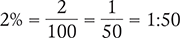
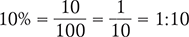
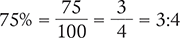
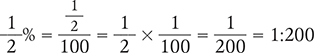
Example 2.2.6
A prescriber ordered a 0.02% solution. You have a 1:1,000 solution; a 1:5,000 solution; and a 1:10,000 solution in stock. Which one of these solutions will fill the order?
To begin, convert the percent to an equivalent fraction. By definition, a percent solution is written in grams per 100 mL (g/100 mL).
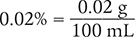
As you know, you can multiply any number by 1 (or a fraction that is equivalent to 1) without changing its value. Therefore, you want to multiply the fraction above by creating a fraction that is equivalent to 1.
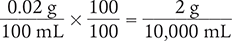
Next, you can reduce 2 g/10,000 mL to 1 g/5,000 mL.
Finally, you can convert the fraction 1 g/5,000 mL to a ratio: 1:5,000.
Answer: The 1:5,000 solution can be used to fill the order for a 0.02% solution.
A solution commonly used for cleaning in healthcare facilities is a 1:10 dilution (10%) of bleach and water. This solution is available commercially or may be prepared daily using regular bleach. Figure 2.3 shows a recipe for making a 10% bleach solution. In the recipe, one part bleach is mixed with nine parts of water. The amounts can be adjusted, but the ratio should not change. Because it chemically degrades, a bleach solution prepared according to this recipe expires after one day.
Figure 2.3 Recipe for a 10% Bleach Solution
The master formula provides a recipe or a set of instructions for preparing a 10% bleach solution.
Example 2.2.7
You have been asked to prepare 480 mL of a 10% bleach solution. Convert this percent to an equivalent fraction reduced to its lowest terms. Then determine how much bleach and water you will need to measure.
To begin, convert 10% to an equivalent ratio. Recall that a percent solution, by definition, is listed in grams per 100 milliliters (g/100 mL).
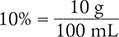
Next, reduce the fraction to its lowest terms.
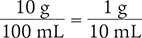
Now, rewrite this fraction as a ratio.
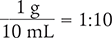
Next, determine the size of one “part” by dividing 10 parts into the total volume.
total volume ÷ number of parts = volume per one part
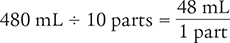
You know from the recipe in Figure 2.3 that the water-bleach solution (total volume) contains a bleach volume that is equal to one part, or 48 mL. Therefore, determine the amount of water needed by subtracting the known bleach volume from the total volume.
total volume − bleach volume = water volume
480 mL − 48 mL = 432 mL
Answer: A 10% bleach solution contains 1 g of bleach per 10 mL. To make 480 mL of 10% bleach solution, combine 48 mL of bleach and 432 mL of water.
Converting a Percent to a Decimal
To convert a percent to a decimal, you drop the percent sign and divide the number by 100. Dividing a number by 100 is equivalent to moving the decimal point two places to the left, inserting zeros if necessary.
4% = 4 ÷ 100 = 0.04
15% = 15 ÷ 100 = 0.15
200% = 200 ÷ 100 = 2.0
Math Morsel
When converting a percent to a decimal, pharmacy technicians should remember to insert zeros—including a leading zero—if necessary.
Converting a Decimal to a Percent
To change a decimal to a percent, you multiply by 100 or move the decimal point two places to the right. Then add a percent sign.
0.25 = 0.25 × 100 = 25%
1.35 = 1.35 × 100 = 135%
0.015 = 0.015 × 100 = 1.5%
2.2 Problem Set
Express the following fractions as percents. Round your answers to the nearest whole percent.
Express the following ratios as percents. Round your answers to the nearest tenth of a percent.
2:3
1.5:4.65
1:250
1:10,000
1:6
Convert the following percents to fractions; then reduce the fractions to their lowest terms.
50%
2%
Convert the following percents to decimals.
6%
12.5%
126%
Perform the following calculations and round your answers to the nearest hundredth when necessary.
5% of 20
20% of 60
19% of 63
110% of 70
0.2% of 50
Fill in the missing values.
|
Percent |
Fraction |
Ratio |
Decimal |
21. |
33% |
|
_____ |
_____ |
22. |
2.5% |
_____ |
1:40 |
_____ |
23. |
_____ |
|
_____ |
0.5 |
24. |
_____ |
_____ |
1:100 |
0.01 |
25. |
90% |
_____ |
_____ |
0.90 |
26. |
67% |
_____ |
_____ |
0.67 |
27. |
_____ |
|
1:500 |
_____ |
28. |
0.45% |
_____ |
_____ |
0.0045 |
29. |
5% |
_____ |
1:20 |
_____ |
30. |
20% |
|
_____ |
_____ |
Applications
Choose the appropriate solution from the available stock solutions.
A 1:10,000 solution has been ordered. You have a 0.05% solution, a 0.01% solution, and a 1% solution in stock. Which solution should you choose?
A 1:20 solution has been ordered. You have a 5% solution, a 10% solution, and a 20% solution in stock. Which solution should you choose?
A 1:25 solution has been ordered. You have a 0.4% solution, a 0.05% solution, and a 4% solution in stock. Which solution should you choose?
A 1:800 solution has been ordered. You have a 0.01% solution, a 0.125% solution, and a 1.25% solution in stock. Which solution should you choose?
A 1:10 solution has been ordered. You have a 0.09% solution, a 0.01% solution, and a 10% solution in stock. Which solution should you choose?
Self-check your work in Appendix A.