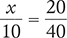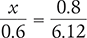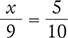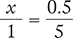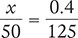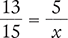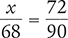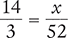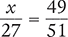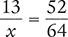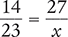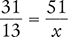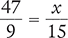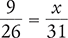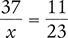2.3 Proportions
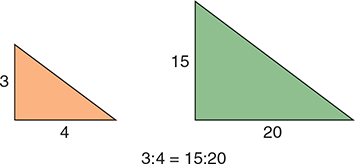
A proportion is an expression of equality between two ratios. This expression can be visualized by thinking of two triangles that have the same shape but are different sizes. The triangles in Figure 2.4 have equal proportions.
Figure 2.4 Triangles with Equal Proportions
These two triangles have equal proportions because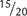 
can be reduced to its lowest terms: ¾.
A proportion can be written three ways: using an equal sign between the ratios, using a double colon (::) between the ratios, or writing the ratios as fractions, as shown below.
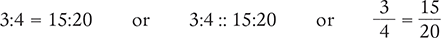
In a proportion, the first and fourth, or outside, numbers are called the extremes. The second and third, or inside, numbers are called the means.
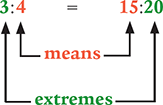
The product of the means must always equal the product of the extremes in a proportion. You can check the accuracy of a proportion by using this formula.
Given a proportion
a:b = c:d
the product of means = the product of extremes
or
b × c = a × d
Example 2.3.1
Confirm that the proportion 3:4 equals the proportion 15:20.
If the two proportions are equal, the product of the means should equal the product of the extremes.
To begin, write the proportions as if they were equal to one another.
3:4 = 15:20
Next, calculate the product of the means (4 and 15) and the product of the extremes (3 and 20).
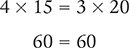
Answer: Because the product of the means equals the product of the extremes, the ratios 3:4 and 15:20 are proportional.
The ratio-proportion method is one of the most frequently used methods for calculating medication doses in a pharmacy. You can use this method any time one ratio is complete and the other ratio has a missing component. In other words, if you know three of the four values in a proportion, you can solve for the missing value. You must also ensure that the numbers remain in the correct proportion to one another and that the numbers have the correct units of measurement in both the numerator and the denominator. Table 2.2 lists the rules for using the ratio-proportion method.
Put Down Roots
The word ratio is a Latin term meaning “to reason or calculate.” The word proportion also has its roots in Latin, with the phrase pro portione meaning “for or according to the relation of parts.” Thus, the ratio-proportion method is based on calculating the relationship of parts to each other.
Table 2.2 Rules for Using the Ratio-Proportion Method
Rule 1. Three of the four amounts must be known. Rule 2. The numerators must have the same unit of measurement. Rule 3. The denominators must have the same unit of measurement. |
Once you learn the ratio-proportion method for solving pharmacy calculations, you can use this method to calculate a medication dose. Table 2.3 lists the steps for using the ratio-proportion method to solve for an unknown quantity, typically designated by the letter x.
Table 2.3 Steps for Using the Ratio-Proportion Method
Step 1. Create a proportion by placing the ratios in fraction form and use a variable (typically, the letter x) to represent the unknown quantity. Step 2. Check that the unit of measurement in the numerators is the same and the unit of measurement in the denominators is the same. Step 3. Use the means–extremes property of proportions to cross multiply and solve for the unknown variable. Step 4. Check your answer by seeing whether the product of the means equals the product of the extremes. |
WORKPLACE WISDOM
When performing ratio-proportion calculations, you can choose where to place the unknown variable (typically represented by the letter x) in the equivalent proportion. In fact, the unknown variable x can appear in all four possible positions, as long as the units in the numerators and the denominators match. However, you may find it helpful to place the unknown variable x in the same location. For example, some pharmacy technicians choose to always place the unknown variable x in the numerator on the left side of the equal sign. The equivalent proportion below uses this format to determine how many milligrams (mg) are in 2 grams (g). Note that the units in the numerators (milligrams) and the denominators (grams) are the same.
Example 2.3.2
A medication is available as 250 mg/5 mL. How many milliliters represent a dose of 375 mg?
You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
To begin, create a proportion by placing the ratios in fraction form and use a variable (the letter x in this example) to represent the unknown quantity.
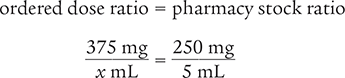
Note that the proportion could be written in several additional ways.
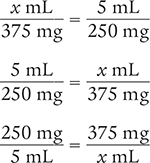
These proportions are all acceptable and could be used to solve for the unknown variable x in this example.
Next, check that the unit of measurement in the numerators is the same and the unit of measurement in the denominators is the same. The numerators have the same unit of measurement (milligrams), and the denominators have the same unit of measurement (milliliters).
Now, use the means–extremes property of proportions to cross multiply and solve for the unknown variable x.
x mL (250 mg) = 5 mL (375 mg)
Next, divide each side of the equation by 250 mg to isolate the unknown variable (x mL). Then cancel like terms and solve for x.
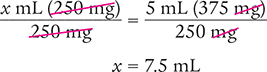
Verify your answer by checking that the product of the means equals the product of the extremes.
Dimensional Analysis Method
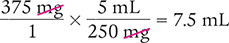
Answer: To deliver a dose of 375 mg of medication, you would need 7.5 mL.
Example 2.3.3
The label shown below is the available stock medication for gentamicin. How many milliliters will need to be prepared if a patient is prescribed 50 mg?
You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
To begin, set up a proportion of the ordered dose (50 mg) over the unknown quantity (x mL) on the left side of the equation, and the available stock medication (20 mg/2 mL) on the right side of the equation. Check that the units of measurement are the same in the numerators (milligrams) and in the denominators (milliliters).
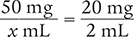
Next, use the means–extremes property of proportions to cross multiply.
x mL (20 mg) = 2 mL (50 mg)
Then solve for x by dividing each side of the equation by 20 mg and canceling the similar units (like units) in the numerators and in the denominators.
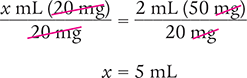
Verify your answer by checking that the product of the means equals the product of the extremes.
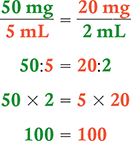
Dimensional Analysis Method
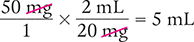
Answer: To fulfill an order for 50 mg, you will need to prepare 5 mL of gentamicin.
Example 2.3.4
The label shown below is the available stock medication. How many milligrams of diazepam will need to be dispensed if a patient is prescribed 4 mL?
You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
Set up a proportion of the unknown quantity (x mg) over the ordered dose (4 mL) on the left side of the equation, and the available stock (5 mg/1 mL) on the right side of the equation. Be sure to check that the unit of measurement in the numerators is the same (milligrams) and that the unit of measurement in the denominators is the same (milliliters).
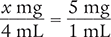
Because these fractions are equivalent, you can cross multiply and the equations will still equal one another.
x mg (1 mL) = 5 mg (4 mL)
Then solve for the unknown variable x by dividing each side of the equation by 1 mL and canceling the similar units (like units) in the numerators and in the denominators.
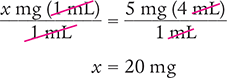
Verify your answer by checking that the product of the means equals the product of the extremes.
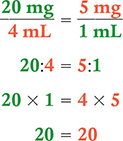
Dimensional Analysis Method
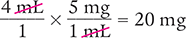
Answer: You will need to dispense 20 mg of diazepam to fill the ordered medication.
In addition to being useful for calculating drug doses in the pharmacy, the ratio-proportion method can be used for converting between units of measurement. To solve a conversion problem, use a conversion factor as one of the proportions. A conversion factor is an equivalency equal to 1. For example, because 1 g = 1,000 mg, you can use the conversion factors 1 g/1,000 mg or 1,000 mg/1 g to solve a pharmacy calculations problem. Additional conversion factors are presented in Appendix C.
WORKPLACE WISDOM
Conversion factors are extremely helpful in pharmacy calculations. Although it is not necessary to memorize all the conversion factors in Appendix C, you may find it helpful to memorize the ones commonly used in most practice settings. For example, the conversion factor of 1 kg = 2.2 lb (written as the ratio 1 kg/2.2 lb) is used in community and institutional pharmacy practice to convert weight. The same can be said for the conversion factor for height: 1 in. = 2.54 cm (written as the ratio 1 in./2.54 cm).
Example 2.3.5
How many milligrams are equivalent to 3 g?
You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Math Morsel
When setting up a proportion to solve a conversion, the units in the numerators must match, and the units in the denominators must match.
Ratio-Proportion Method
To begin, set up a proportion of the unknown quantity (x mg) over the unit of measurement (3 g) on the left side of the equation, and the conversion factor of milligrams to grams (1,000 mg/1 g) on the right side of the equation. Be sure to check that the unit of measurement in the numerators is the same (milligrams) and that the unit of measurement in the denominators is the same (grams).
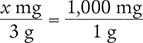
Because these fractions are equivalent, you can cross multiply and the equations will still equal one another.
x mg (1 g) = 1,000 mg (3 g)
Then solve for x by dividing each side of the equation by 1 g and canceling the similar units (like units) in the numerators and in the denominators.
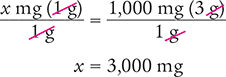
Verify your answer by checking that the product of the means equals the product of the extremes.
Dimensional Analysis Method
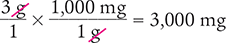
Answer: There are 3,000 mg in 3 g.
Example 2.3.6
Convert 44 lb to kilograms. Refer to Appendix C to determine the conversion from pounds (lb) to kilograms (kg).
This example requires you to convert a unit in the household measurement system (pounds) to a unit in the metric measurement system (kilograms). You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
To begin, set up a proportion of the unknown quantity (x kg) over the known measurement (44 lb) on the left side of the equation. Then use the conversion you found in Appendix C (2.2. lb = 1 kg) to create a fraction (1 kg/2.2 lb) on the right side of the equation. Note that you must arrange the conversion factor so that similar units (like units) appear in the numerators (kilograms) and in the denominators (pounds).
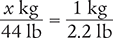
Next, cross multiply the equivalent fractions.
x kg (2.2 lb) = 1 kg (44 lb)
Then solve for x by dividing each side of the equation by 2.2 lb and canceling the similar units (like units) in the numerators and in the denominators.
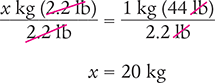
Verify your answer by checking that the product of the means equals the product of the extremes.
Dimensional Analysis Method
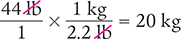
Answer: The weight of 44 lb in the household measurement system converts to 20 kg in the metric measurement system.
The ratio-proportion method can also be used to solve many types of percent problems. When setting up the ratios, remember that a percent may be written in fraction form, with the percent value over 100. For example, 95% is equivalent to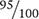 
.
Example 2.3.7
A patient needs to take 75% of a recommended dose before the medication may be discontinued. The recommended dose is 650 mg. How many milligrams of medication must the patient take before it is discontinued?
You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
To begin, place the unknown variable (x mg) over the recommended dose (650 mg) on the left side of the equation. Then write the percent (75%) as a fraction (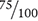
) on the right side of the equation.
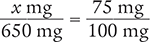
Be sure to check that the unit of measurement in the numerators is the same (milligrams) and that the unit of measurement in the denominators is the same (milligrams).
Next, cross multiply the equivalent fractions.
x mg (100 mg) = 650 mg (75 mg)
Then solve for x by dividing each side of the equation by 100 mg and canceling the similar units (like units) in the numerators and in the denominators.
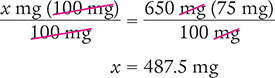
Verify your answer by checking that the product of the means equals the product of the extremes.
Dimensional Analysis Method
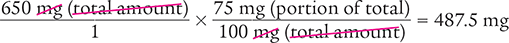
Answer: To take 75% of the recommended dose, the patient must take 487.5 mg of the medication.
Example 2.3.8
A patient has taken 85% of a recommended dose of medication. If the amount taken is 320 mg, what was the recommended dose?
Another way of phrasing this question is as follows: “320 mg is 85% of what amount?”
You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
To begin, set up two equivalent proportions based on the information given.
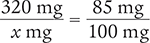
Be sure to check that the unit of measurement in the numerators is the same (milligrams of the portion of the whole) and that the unit of measurement in the denominators is the same (milligrams of the total amount).
Next, cross multiply the equivalent fractions.
x mg (85 mg) = 320 mg (100 mg)
Then solve for x by dividing each side of the equation by 85 mg and canceling the similar units (like units) in the numerators and in the denominators.
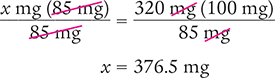
Verify your answer by checking that the product of the means equals the product of the extremes.
Dimensional Analysis Method
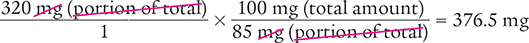
Answer: The recommended dose of the medication was 376.5 mg.
2.3 Problem Set
Solve for the unknown variable x in each of the following proportions. Round your answers to the nearest hundredth when necessary.
Set up ratio-proportion problems to solve for the unknown variable x. Round your answers to the nearest hundredth.
72 is what percent of 254?
90% of what number is 44?
44% of what number is 100?
28% of what number is 34?
24.5 is what percent of 45?
Change the following weights using the conversion factor 1 g = 1,000 mg.
100 mg = ____________ g
247 mg = ____________ g
1,420 mg = ____________ g
495 mg = ____________ g
3,781 mg = ____________ g
0.349 g = ____________ mg
1.5 g = ____________ mg
0.083 g = ____________ mg
0.01 g = ____________ mg
2.1 g = ____________ mg
Change the following weights using the conversion factor 1 kg = 2.2 lb. Round your answers to the tenths place.
6.3 lb = ____________ kg
15 lb = ____________ kg
97 lb = ____________ kg
115 lb = ____________ kg
186 lb = ____________ kg
7.5 kg = ____________ lb
3.6 kg = ____________ lb
79.2 kg = ____________ lb
90 kg = ____________ lb
0.5 kg = ____________ lb
Applications
Use the ratio-proportion method to solve the following problems.
Progesterone is available as 50 mg/mL. The order calls for 100 mg of progesterone. How many milliliters will you prepare?
Capicillin is available as a 125 mg tablet. How many tablets are needed to provide a dose of 375 mg?- Soakamycin is available as a concentration of 20 mg/mL. How many milliliters are needed to prepare a foot soak that contains 300 mg?
You are going to buy some folders to file your orders. After doing research, you find that the most cost-effective price is $7.40 per box of 100 folders. You have $15 to spend. How many 100-count boxes can you buy?
A patient is to receive an intramuscular injection of 10,000 units of Musclesporin. You have a bottle containing 250,000 units per 15 mL. How many milliliters must be prepared to administer this dose?A prescriber ordered a dose of 30 mg of gentamicin. The medication is available as a 20 mg/2 mL solution. How many milliliters are needed to provide the ordered dose?
A prescriber ordered a dose of 60 mg of famotidine. The medication is available as a 40 mg/4 mL solution. How many milliliters are needed to provide the ordered dose?
A prescriber ordered a dose of 300 mg. The medication is available as a 500 mg/10 mL solution. How many milliliters are needed to provide the ordered dose?
A prescriber ordered a dose of 30 mg of lamivudine oral solution. The medication is available as a 5 mg/mL oral solution. How many milliliters are needed to provide the ordered dose?
A prescriber ordered a dose of 30 mg. The medication is available as a 20 mg/mL solution. How many milliliters are needed to provide the ordered dose?
Use the following medication label to determine the doses needed for questions 51–55.
The order calls for 5 mL of furosemide. How many milligrams will the patient receive in the ordered amount?
The order calls for 80 mg of furosemide. How many milliliters are needed to fill the order?
The order calls for 50 mg of furosemide. How many milliliters are needed to fill the order?
The order calls for 12.5 mg of furosemide. How many milliliters are needed to fill the order?
The order calls for 3.5 mL of furosemide. How many milligrams will the patient receive in the ordered amount?
Self-check your work in Appendix A.