2.4 Percentage of Error
Percentage has applications in pharmacy beyond what has been discussed previously in this chapter. Measurement accuracy is one such application. When measuring a substance, the measuring device will approximate the actual amount to a certain degree of accuracy. Percentage of error is a way of expressing the difference between a known or desired value and its measured value. In other words, percentage of error tells you how close your measured value is to its true value.
Percentage of error is used to determine the accuracy of two measuring devices commonly used in a pharmacy: graduates and prescription balances. Regardless of the measuring device, it is important for you to know the margin of error associated with a particular graduate or prescription balance.

Graduated cylinders are used to accurately measure liquids in the pharmacy.

A Class III torsion prescription balance can accurately weigh small quantities.
Graduates are instruments used for liquid volume measurements. In pharmacy practice, the graduates may be cylindrical or conical in shape. Graduated cylinders are more commonly used as they are typically more accurate. A graduated cylinder has marks, or graduations, in increments (usually milliliters). Although not all graduated cylinders are equally accurate, these measuring devices are more accurate than the household measuring devices used by patients at home.
Prescription balances are used to measure weights in the pharmacy. The most common balance in pharmacies is the Class III torsion prescription balance. This balance uses a two-pan torsion system that requires both internal and external weights. Typically, this balance may be used only to weigh masses ≥ 120 mg and no more than 60 g or 120 g, depending on the balance. Although Class III balances are generally accurate when compared with other small scales, these balances may exhibit slight variations.
Although graduated cylinders and Class III torsion prescription balances are used to improve measurement accuracy, all measuring instruments have limitations. Imagine that you want to measure 50 mL of water in a graduated cylinder. Even if you have stellar measuring technique and painstakingly attempt to measure 50 mL, there is still error due to the precision of the measuring device. This amount of error can be determined using the percentage of error formula.
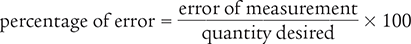
In the preceding formula, the term error of measurement is the difference between the measured value and the quantity desired.
 Safety Alert
Safety Alert
Percentage of error in measurement may seem unimportant. However, there are medications that require extremely precise dosing. For these medications, small changes (either too much or too little) can seriously affect patient safety and outcomes.
error of measurement = measured value − quantity desired
In pharmacy calculations, it is typical to report percentage of error as a positive integer.
Consider the following situation. You are to dispense 50 mL of cetirizine solution. The original measurement shows 50 mL. When you verify the amount using a more accurate graduated cylinder, the actual amount is 52 mL. The error of measurement in this example is the difference between the measured value and the quantity desired.
52 mL − 50 mL = 2 mL
Now that you know the error of measurement, you can calculate the percentage of error.
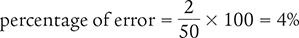
The following examples further illustrate how to calculate percentage of error.
Example 2.4.1

You are to dispense 50 mL of cetirizine solution. The original measurement shows 50 mL. When you verify the amount using a more accurate graduated cylinder, the actual amount is 54 mL. What is the error of measurement?
To begin, use the following formula to determine the error of measurement.
measured value − quantity desired = error of measurement
Then calculate the difference between the measured value (54 mL) and the quantity desired (50 mL) to determine the error of measurement.
54 mL − 50 mL = 4 mL
Answer: The error of measurement is 4 mL.
Example 2.4.2
You are to dispense 120 mL of a liquid. The original measurement is 120 mL. When you verify the amount using a more accurate graduated cylinder, the measured amount is 126 mL. What is the percentage of error of the original measurement?
To begin, determine the error of measurement by using the following formula.
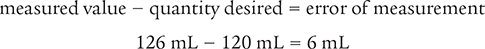
Next, use the percentage of error equation to determine the percentage of error of the measurement.
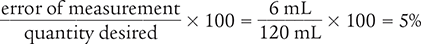
Answer: The percentage of error of the original measurement is 5%.
Example 2.4.3
You are to dispense 30 g of a powder. The original measurement is 30 g. When you verify the amount using a more accurate balance, the actual amount is 31.8 g. What is the percentage of error of the original measurement?
To begin, calculate the difference in the two amounts to determine the error of measurement.
31.8 g − 30 g = 1.8 g
Then use the percentage of error equation to determine the percentage of error of the measurement.
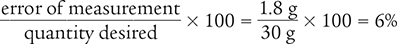
Answer: The percentage of error of the original measurement is 6%.
Example 2.4.4
You are to dispense 453 mg of a powder. The original measurement is 453 mg. When you verify the amount using a more accurate balance, the actual amount is 438 mg. What is the percentage of error of the original measurement?
To begin, calculate the difference in the two measurements to determine the error of measurement.
438 mg − 453 mg = −15 mg
Next, take the absolute value of −15, which is 15.
Finally, use the percentage of error equation to determine the percentage of error of the measurement.
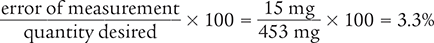
Answer: The percentage of error of the original measurement is 3.3%.
A concept related to percentage of error is error tolerance. Error tolerance is the acceptable amount of error allowed in measurements. The range of error tolerance varies based on your practice setting.
Consider a setting with a 5% range of error tolerance. This range means that a measured quantity must be within 5% of the desired quantity. For a desired quantity of 100 g, the measured quantity must be between 95 g and 105 g to be acceptable within the 5% range of error tolerance. The following examples utilize error tolerance and its application in pharmacy practice.
Example 2.4.5
You are to weigh 60 g of a cream base for a topical compound. Your error tolerance range is 3%. What will be the lower weight limit (in grams) and the upper weight limit (in grams) that would be within the 3% error tolerance range?
To begin, convert the error tolerance range (3%) to a decimal: 0.03. Then multiply the target weight (60 g) by the error tolerance range.
60 g × 0.03 = 1.8 g
Next, determine the lower and upper limits of the error range by subtracting and adding 1.8 g to your target weight of 60 g.
60 g − 1.8 g = 58.2 g 60 g + 1.8 g = 61.8 g
Answer: To be within the 3% error tolerance range, your lower weight limit for the cream base would be 58.2 g, and your upper weight limit would be 61.8 g.
Example 2.4.6
You are preparing an order by measuring 800 mL from a 1 liter (L) normal saline IV bag. When you verify the volume of the fluid in a graduated cylinder, the amount measured is actually 820 mL. What is the percentage of error in this measurement? If your error tolerance range is 2%, is your measurement acceptable?
To begin, find the difference in the two measurements to determine the error of measurement.
820 mL − 800 mL = 20 mL
Then use the percentage of error equation to determine the percentage of error of the measurement.
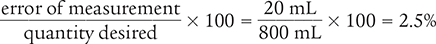
Answer: Because 2.5% is larger than the acceptable error tolerance range of 2%, the target range was not met.
2.4 Problem Set
Calculate the percentage of error for the following measurements. Then round your answers to the nearest hundredth when necessary.
The desired weight is 185 mg, but the measured weight is 189 mg.
The desired weight is 500 mg, but the measured weight is 476 mg.
The desired weight is 1,200 mg, but the measured weight is 1,507 mg.
The desired weight is 15 mg, but the measured weight is 12.5 mg.
The desired weight is 400 mcg, but the measured weight is 415 mcg.
The desired volume is 5 mL, but the measured volume is 6.3 mL.
The desired volume is 15 mL, but the measured volume is 13 mL.
The desired volume is 15 mL, but the measured volume is 20 mL.
The desired volume is 1.5 L, but the measured volume is 1.45 L.
The desired volume is 700 mL, but the measured volume is 726 mL.
Determine the percentage of error for the following measurements, and identify whether or not your answers fall within the error tolerance range of 3%.
The desired volume is 3 mL, but the measured volume is 2.6 mL.
The desired volume is 12.5 mL, but the measured volume is 12.1 mL.
The desired volume is 1.8 mL, but the measured volume is 1.5 mL.
The desired volume is 3.2 mL, but the measured volume is 3.29 mL.
Determine the percentage of error for the following measurements, and identify whether or not your answers fall within the error tolerance range of 5%.
The desired weight is 150 mg, but the measured weight is 149 mg.
The desired weight is 200 mg, but the measured weight is 192 mg.
The desired weight is 30 mg, but the measured weight is 31.5 mg.
The desired weight is 454 mg, but the measured weight is 450 mg.
State the acceptable error tolerance range for the following measurements. Round your answers to the nearest hundredth as needed.
The desired volume is 200 mL, and the error tolerance is 0.5%.
The desired volume is 10.3 mL, and the error tolerance is 0.75%.
The desired volume is 830 mL, and the error tolerance is 2%.
The desired weight is 18 g, and the error tolerance is 0.15%.
The desired weight is 750 mg, and the error tolerance is 0.4%.
Applications
If a generic drug manufacturer meets a bioavailability (the degree to which a drug becomes available to the target tissue after administration) comparison to within 20%, and a drug typically has a bioavailability of 100 mg, what is the acceptable range?
The drug manufacturer of a new brand of vitamin C tablets claims that its product has a bioavailability within 12% of an established brand of vitamin C tablets. The established brand has 500 mg of vitamin C per tablet. What is the acceptable range of vitamin C contained in the new brand of tablet?
Self-check your work in Appendix A.