4.2 Conversions within the Metric Measurement System
To convert units within the metric measurement system, you have three options: multiplying or dividing (moving the decimal point), using the ratio-proportion method, or using the dimensional analysis method. Once you learn the three methods of conversion, you may want to select the most comfortable method and use only that method when making conversions.
Multiplying or Dividing (Moving the Decimal Point)
To change the metric units of a number to smaller or larger units, you can multiply or divide by an appropriate multiple of 1,000 (see Table 4.4). You use multiplication to convert a larger metric unit of measurement to a smaller metric unit of measurement. For example, to convert 5 g to milligrams (mg), you need to know the following metric conversion: 1 g equals 1,000 mg. Therefore, you multiply 5 by 1,000 to get 5,000 mg. You can also multiply by 1,000 by moving the decimal point three places to the right: 5.0 becomes 5000, or 5,000. To convert 17 L to microliters (mcL), you need to know the following metric conversion: 1 L equals 1,000,000 mcL. Therefore, you multiply 17 by 1,000,000 to get 17,000,000 mcL. You can also multiply by 1,000,000 by moving the decimal point six places to the right: 17.0 becomes 17000000, or 17,000,000.
Table 4.4 Metric Unit Equivalents
| Kilo | Base | Milli | Micro |
|---|---|---|---|
0.001 kg |
1 g |
1,000 mg |
1,000,000 mcg |
0.001 kL |
1 L |
1,000 mL |
1,000,000 mcL |
0.001 km |
1 m |
1,000 mm |
1,000,000 mcm |
Conversely, you use division to convert a smaller metric unit of measurement to a larger metric unit of measurement. For example, to convert 3 grams (g) to kilograms (kg), you need to know the following metric conversion: 1,000 g equals 1 kg. Therefore, you divide 3 by 1,000 to get 0.003 kg. You can also divide by 1,000 by moving the decimal point three places to the left: 3.0 becomes 0.003. To convert 22 mL to liters (L), you need to know the following metric conversion: 1,000 mL equals 1 L. Therefore, you divide 22 by 1,000 to get 0.022 L. You can also divide by 1,000 by moving the decimal point three places to the left: 22.0 becomes 0.022.
 Math Morsel
Math Morsel
Moving the decimal point three places to the right is the same as multiplying by 1,000. Moving the decimal point three places to the left is the same as dividing by 1,000.
The key to understanding the relationships of the prefixes kilo–, milli –, and micro– to a base unit in the metric system is to remember that the decimal point must be moved three places when converting from one unit to the next. Moving the decimal point three places is a quick way to multiply or divide the number by 1,000. The three places are representative of the three zeros in 1,000. Table 4.5 summarizes the conversions of common metric units using multiplication, division, and movement of the decimal point.
Table 4.5 Common Metric Conversions
Conversion |
Instruction |
Example |
|---|---|---|
kilograms (kg) to grams (g) |
multiply by 1,000 (move decimal point three places to the right) |
6.25 kg = 6,250 g |
grams (g) to milligrams (mg) |
multiply by 1,000 (move decimal point three places to the right) |
3.56 g = 3,560 mg |
milligrams (mg) to grams (g) |
divide by 1,000 (move decimal point three places to the left) |
120 mg = 0.120 g |
liters (L) to milliliters (mL) |
multiply by 1,000 (move decimal point three places to the right) |
2.5 L = 2,500 mL |
milliliters (mL) to liters (L) |
divide by 1,000 (move decimal point three places to the left) |
238 mL = 0.238 L |
The following examples show the conversion of a smaller metric unit of measurement to a larger metric unit of measurement. Remember that this type of conversion requires you to move the decimal point three places to the left.
Example 4.2.1
Convert 4,500 mL to liters.
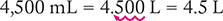
Answer: A volume of 4,500 mL is equal to 4.5 L.
Example 4.2.2
Convert 1,287 mg to grams.
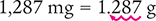
Answer: A weight of 1,287 mg is equal to 1.287 g.
Example 4.2.3
Convert 480 mL to liters.

Answer: A volume of 480 mL is equal to 0.48 L.
The following examples show the conversion of a larger metric unit of measurement to a smaller metric unit of measurement. Remember that this type of conversion requires you to move the decimal point three places to the right.
Example 4.2.4
Convert 0.954 g to milligrams.
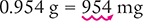
Answer: A weight of 0.954 g is equal to 954 mg.
Example 4.2.5
Convert 1.5 g to milligrams.
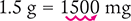
Answer: A weight of 1.5 g is equal to 1,500 mg.
Example 4.2.6
Convert 0.621 mg to micrograms.
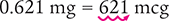
Answer: A weight of 0.621 mg is equal to 621 mcg.
 WORKPLACE WISDOM
WORKPLACE WISDOM
At first, it may be difficult to visualize conversions from smaller to larger units. It can be helpful to think about this concept in terms of more familiar units. Suppose you have $1,000,000 all in one-dollar bills (a smaller unit). In other words, you have 1,000,000 one-dollar bills. Suppose you wanted larger units and exchanged your dollar bills for $100 bills. You would then have 10,000 one-hundred-dollar bills (move the decimal point two places to the left). Now suppose you exchange all your $100 bills for $1,000 dollar bills (assume that one-thousand-dollar bills are still printed). You would have 1,000 one-thousand-dollar bills (move the decimal point one place to the left). In the end, you have the same amount of total dollars ($1,000,000), but you changed the units from smaller (one-dollar bills) to larger (one-hundred-dollar bills and then one-thousand-dollar bills).
Using the Ratio-Proportion Method
If you have difficulty remembering which way to move the decimal point when converting between units of measurement in the metric system, the ratio-proportion method introduced in Chapter 2 is an effective alternative. This method is a foolproof way to convert metric units. Set up the conversion by placing the unknown variable x and the value to be converted on the left side of the equation and the conversion factor (the ratio of the desired unit to the given unit) on the right side of the equation.
When setting up a proportion to solve for the unknown variable x, remember that the units in the numerators must match and the units in the denominators must match. Checking to make sure that the units match before completing the calculation will ensure accuracy in the conversion. The next examples demonstrate conversions by moving the decimal point, followed by the same conversions using the ratioproportion method.
 Math Morsel
Math Morsel
When setting up proportions, units in the numerators must match, and units in the denominators must match.
Example 4.2.7
Convert 2,300 mg to grams.
To perform this conversion, you can use two methods: multiplying or dividing (moving the decimal point) or using the ratio-proportion method.
Multiplying or Dividing (Moving the Decimal Point)
To begin, recognize that you are converting a smaller unit (milligrams) to a larger unit (grams). Then you can either divide by 1,000 or move the decimal point three places to the left, as shown below.
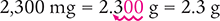
Ratio-Proportion Method
To begin, set up a proportion by placing the unknown variable x over the value to be converted (2,300 mg) on the left side of the equation. Then place the conversion factor (1 g equals 1,000 mg) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
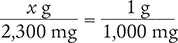
Now, cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
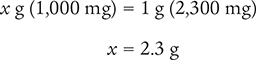
Answer: The conversion indicates that 2,300 mg is equal to 2.3 g.
 Math Morsel
Math Morsel
Pharmacy technicians who use the ratio-proportion method can verify their answer by multiplying the means and the extremes in the ratio. The products of the means and of the extremes must be equal.
Example 4.2.8
Convert 3.2 mg to micrograms.
To perform this conversion, you can use two methods: multiplying or dividing (moving the decimal point) or using the ratio-proportion method.
Multiplying or Dividing (Moving the Decimal Point)
To begin, recognize that you are converting a larger unit (milligrams) to a smaller unit (micrograms). Then multiply by 1,000 or move the decimal point three places to the right, as shown below.
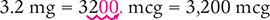
Ratio-Proportion Method
To begin, set up a proportion by placing the unknown variable x over the value to be converted (3.2 mg) on the left side of the equation. Then place the conversion factor (1,000 mcg equals 1 mg) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
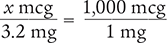
Now, cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
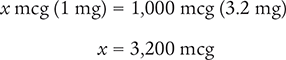
Answer: The conversion indicates that 3.2 mg is equal to 3,200 mcg.
Example 4.2.9
Convert 3.785 L to milliliters.
To perform this conversion, you can use two methods: multiplying or dividing (moving the decimal point) or using the ratio-proportion method.
Multiplying or Dividing (Moving the Decimal Point)
To begin, recognize that you are converting a larger unit (liters) to a smaller unit (milliliters). Then multiply by 1,000 or move the decimal point three places to the right, as shown below.
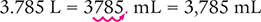
Ratio-Proportion Method
To begin, set up a proportion by placing the unknown variable x over the value to be converted (3.785 L) on the left side of the equation. Then place the conversion factor (1,000 mL equals 1 L) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
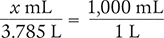
Now, cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
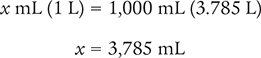
Answer: The conversion indicates that 3.785 L is equal to 3,785 mL.
Example 4.2.10
Convert 454 g to kilograms.
To perform this conversion, you can use two methods: multiplying or dividing (moving the decimal point) or using the ratio-proportion method.
Multiplying or Dividing (Moving the Decimal Point)
To begin, recognize that you are converting a smaller unit (grams) to a larger unit (kilograms). Then divide by 1,000 or move the decimal point three places to the left, as shown below.
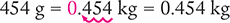
Ratio-Proportion Method
To begin, set up a proportion by placing the unknown variable x over the value to be converted (454 g) on the left side of the equation. Then place the conversion factor (1 kg equals 1,000 g) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
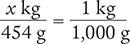
Now, cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
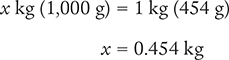
Answer: The conversion indicates that 454 g is equal to 0.454 kg.
Using the Dimensional Analysis Method
As you learned in earlier chapters, the dimensional analysis method is a problem-solving method that uses the math principle that any number or expression can be multiplied by one without changing its value. As a reminder, you can set up the problems so that the starting units cancel one another and, consequently, you are left with the desired units.
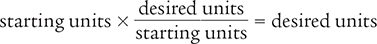
Example 4.2.11
Convert 486 mg to grams.
To begin, you know that the starting units are milligrams (486 mg). You also know that the desired units are grams and that 1 g equals 1,000 mg.
Then use this information to set up your equation. Cancel similar units (like terms) to determine the desired units.
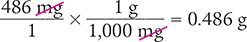
Answer: The conversion indicates that 486 mg is equal to 0.486 g.
Example 4.2.12
Convert 4.5 L to milliliters.
To begin, you know that the starting units are liters (4.5 L). You also know that the desired units are milliliters and that 1,000 mL equals 1 L.
Then use this information to set up your equation. Cancel similar units (like terms) to determine the desired units.
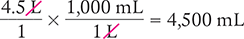
Answer: The conversion indicates that 4.5 L is equal to 4,500 mL.
Example 4.2.13
Convert 240 mL to liters.
To begin, you know that the starting units are milliliters (240 mL). You also know that the desired units are liters and that 1 L equals 1,000 mL.
Then use this information to set up your equation. Cancel similar units (like terms) to determine the desired units.
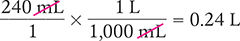
Answer: The conversion indicates that 240 mL is equal to 0.24 L.
Example 4.2.14
Convert 0.725 mg to micrograms.
To begin, you know that the starting units are milligrams (0.725 mg). You also know that the desired units are micrograms and that 1,000 mcg equals 1 mg.
Then use this information to set up your equation. Cancel similar units (like terms) to determine the desired units.
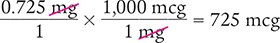
Answer: The conversion indicates that 0.725 mg is equal to 725 mcg.
Example 4.2.15
Convert 0.519 g to micrograms.
To begin, you know that the starting units are grams (0.519 g). You also know that the desired units are micrograms. Therefore, you must perform two conversions.
For the first conversion, you need to change grams to milligrams. You know that 1,000 mg equals 1 g. For the second conversion, you need to change milligrams to micrograms. You know that 1,000 mcg equals 1 mg.
Then use this information to set up your equation. Cancel similar units (like terms) to determine the desired units.
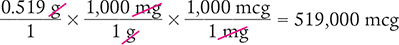
Answer: The conversion indicates that 0.519 g is equal to 519,000 mcg.
4.2 Problem Set
Convert the following units within the metric system by using the ratio-proportion method. Retain all significant figures and do not round your answers.
1,964 mcg = __________ mg
418 mg = _____________ g
651 mg = _____________ mcg
0.84 mg = ____________ mcg
0.012 g = ____________ mcg
9,213,406 mcg = ______ g
284 mg = _____________ g
9,382.5 mcg = ________ mg
12,321 mcg = _________ g
184 g = ______________ kg
Convert the following units within the metric system by using the dimensional analysis method. Retain all significant figures and do not round your answers.
52 mL = ______________ L
2.06 g = _____________ mg
16 mg = ______________ mcg
256 mg = _____________ g
2,703,000 mcg = ______ g
6.9 L = ______________ mL
62.5 mg = ____________ g
15 kg = ______________ g
2,785,000 mcg = ______ g
8.234 mg = ___________ mcg
Convert the following units by moving the decimal point, or by using the method that you prefer. Show all work. Retain all significant figures and do not round your answers.
2 kg = _______________ mg
21 L = _______________ mL
576 mL = _____________ L
823 kg = _____________ mg
27 mcg = _____________ mg
5,000 mcg = __________ mg
20 mcg = _____________ mg
4.624 mg = ___________ mcg
3.19 g = _____________ mg
8,736 mcg = __________ mg
830 mL = _____________ L
0.94 L = _____________ mL
1.84 g = _____________ mg
560 mg = _____________ g
1,200 mcg = __________ mg
125 mcg = ____________ mg
0.275 mg = ___________ mcg
480 mL = _____________ L
239 mg = _____________ g
1,500 mg = ___________ g
Applications
The following prescription has come into your pharmacy. Note: One teaspoon (1 tsp) is equivalent to five milliliters (5 mL).

 Clarithromycin Granules 125 mg/5 mL
Clarithromycin Granules 125 mg/5 mL2 teaspoonfuls bid
 food or fluid for 7 days
food or fluid for 7 daysHow many milliliters will the patient take daily?
How many milliliters should be dispensed to the patient?
How many grams will the patient take daily?
Using the following drug label, how many bottles of clarithromycin will be needed to fill this prescription?.

A patient is to take 1.5 g of amoxicillin before a dental procedure. The capsules available are shown in the following label. How many capsules will be dispensed to this patient?

A patient is to receive 1,000 mg of vancomycin two times daily, diluted in IV solution. The following label shows the stock available.

How many doses are available in one vial?
How many days will one unopened vial last? Assume that the patient is the only one using vancomycin from this vial.
Self-check your work in Appendix A.