4.4 Conversions within the Household Measurement System
Like the metric measurement system, household units of measurement can be converted to larger or smaller units. The following examples demonstrate the conversion of units of volume using both the ratio-proportion method and the dimensional analysis method. Once you learn both methods of conversion, select the method you are most comfortable with and use only that method when making conversions.
Example 4.4.1
How many teaspoonfuls are in 2 tablespoonfuls?
To begin, refer to the appropriate equivalent indicated in Table 4.6 and Figure 4.2.
3 tsp = 1 tbsp
Then use this equivalent when performing the following calculation methods.
Ratio-Proportion Method
To begin, set up a proportion by placing the unknown variable x over the value to be converted (2 tbsp) on the left side of the equation. Then place the conversion factor (3 tsp equals 1 tbsp) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
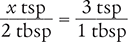
Now, cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.

Dimensional Analysis Method
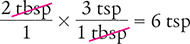
Answer: There are 6 teaspoonfuls in 2 tablespoonfuls.
Example 4.4.2
How many tablespoonfuls are in 2 cups of medication?
To begin, refer to the appropriate equivalents indicated in Table 4.6 and Figure 4.2.
2 tbsp = 1 fl oz
1 cup = 8 fl oz
Then use these equivalents when performing the following calculation methods.
Ratio-Proportion Method
To begin, determine the number of fluid ounces in 2 cups by setting up a proportion. Place the unknown variable x over the value to be converted (2 cups) on the left side of the equation. Then place the conversion factor (8 fl oz equals 1 cup) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
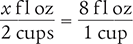
Next, cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
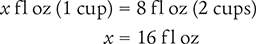
Now, determine the number of tablespoonfuls in 16 fl oz by setting up another proportion. Place the unknown variable x over the value to be converted (16 fl oz) on the left side of the equation. Then place the conversion factor you cited at the beginning of this example (2 tbsp equals 1 fl oz) on the right side of the equation.
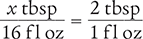
Finally, cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
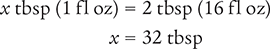
Dimensional Analysis Method
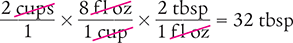
Answer: There are 32 tablespoonfuls in 2 cups of medication.
Example 4.4.3
How many 1 tsp doses are in 3 cups of liquid medication?
To begin, refer to the appropriate equivalents indicated in Table 4.6 and Figure 4.2.
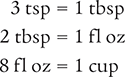
Then use these equivalents when performing the following calculation methods.
Ratio-Proportion Method
To begin, determine the number of fluid ounces in 3 cups by setting up a proportion. Place the unknown variable x over the value to be converted (3 cups) on the left side of the equation. Then place the conversion factor (8 fl oz equals 1 cup) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
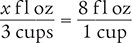
Next, cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
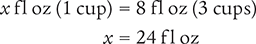
Now, determine the number of tablespoonfuls in 24 fl oz by setting up another proportion. Place the unknown variable x over the value to be converted (24 fl oz) on the left side of the equation. Then place the conversion factor you cited at the beginning of this example (2 tbsp equals 1 fl oz) on the right side of the equation.
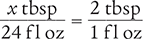
Next, cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
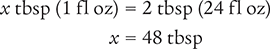
Then determine the number of teaspoonfuls in 48 tablespoonfuls by setting up another proportion. Place the unknown variable x over the value to be converted (48 tbsp) on the left side of the equation. Then place the conversion factor you cited at the beginning of this example (3 tsp equals 1 tbsp) on the right side of the equation.
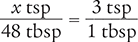
Finally, cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
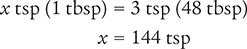
Dimensional Analysis Method
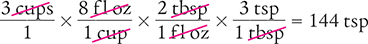
Answer: There are 144 teaspoonfuls in 3 cups of liquid medication.
Example 4.4.4
How many 1 fl oz doses are in 3 pt of liquid medication?
To begin, refer to the appropriate equivalents indicated in Table 4.6 and Figure 4.2.
8 fl oz = 1 cup
2 cups = 1 pt
Then use these equivalents when performing the following calculation methods.
Ratio-Proportion Method
To begin, determine the number of cups in 3 pt by setting up a proportion. Place the unknown variable x over the value to be converted (3 pt) on the left side of the equation. Then place the conversion factor (2 cups equal 1 pt) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
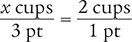
Next, cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
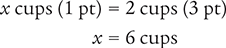
Now, determine the number of fluid ounces in 6 cups by setting up another proportion. Place the unknown variable x over the value to be converted (6 cups) on the left side of the equation. Then place the conversion factor you cited at the beginning of this example (8 fl oz equals 1 cup) on the right side of the equation.
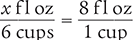
Finally, cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
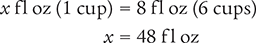
Dimensional Analysis Method
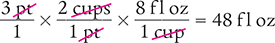
Answer: There are 48 fl oz doses in 3 pt of liquid medication.
Example 4.4.5
How many 1 fl oz doses are in 2 qt of liquid medication?
To begin, refer to the appropriate equivalents indicated in Table 4.6 and Figure 4.2.
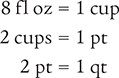
Then use these equivalents when performing the following calculation methods.
Ratio-Proportion Method
To begin, determine the number of pints in 2 qt by setting up a proportion. Place the unknown variable x over the value to be converted (2 qt) on the left side of the equation. Then place the conversion factor (2 pt equal 1 qt) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
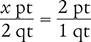
Next, cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
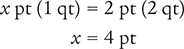
Now, determine the number of cups in 4 pt by setting up another proportion. Place the unknown variable x over the value to be converted (4 pt) on the left side of the equation. Then place the conversion factor you cited at the beginning of this example (2 cups equal 1 pt) on the right side of the equation.
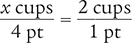
Then cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
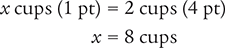
Next, determine the number of fluid ounces in 8 cups.
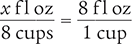
Finally, cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
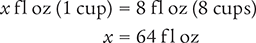
Dimensional Analysis Method
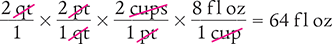
Answer: There are 64 fl oz doses in 2 qt of liquid medication.
4.4 Problem Set
Convert the given volumes within the household measurement system. Round your answers to the nearest tenth when necessary.
8 cups = ____________ pt
3 pt = ______________ fl oz
1 pt = ______________ tbsp
3 qt = ______________ fl oz
28 tsp = ____________ fl oz
1 pt = ______________ qt
6 cups = ____________ tsp
Applications
Complete the following conversions. Round your answers to the nearest tenth when necessary.
How many 1 tsp doses are in 2 pt, 6 fl oz?
How many 2 tsp doses are in 3 cups?
How many 1 tbsp doses are in 12 bottles containing 16 fl oz each?