4.5 Conversions between the Metric and Household Measurement Systems
Because metric system units are more accurate than household system units, it is preferable that you work with metric units in your pharmacy calculations. In addition, some pharmacy software programs accept only amounts given in metric units. With that in mind, you need to be adept at performing conversions between these two measurement systems.
 Quick Study
Quick Study
A pharmacy technician should memorize the approximate equivalent measurements for common units such as the following:
1 m = 3 ft
1 kg = 2.2 lb
1 lb = 454 g
1 oz = 30 mL
When working in an institutional or a long-term care facility, you will see medication orders that are written using both metric and household units of measurement. Typically, computerized provider order entry (CPOE) software is set up to accept metric units. However, in the event household units are used by a prescriber, you must convert the quantity ordered into metric units.
In a community pharmacy, you may also receive prescriptions written in both metric and household units of measurement. For prescriptions written in household units, you should convert any quantity measurements to metric units and then enter the information into the computerized patient’s profile. Typically, the computer software is set up to accept milliliters for liquid medications and grams for solid medications, such as creams or ointments. When a prescription is written for a liquid, the volume to be dispensed and the quantity to be given at each dose is used to calculate the days’ supply. Calculating the volume to be dispensed and the days’ supply are important steps in the processing of each prescription. These calculations provide the pharmacist and you with the information needed to accurately fill the prescription, thereby ensuring that the patient is getting the prescribed therapy.
Although some references list exact values for conversions between the household measurement system and the metric measurement system, the equivalents shown in Table 4.7 and Figure 4.3 on the following page are generally accepted for use for these conversions in daily pharmacy practice. You should commit these conversion values to memory.

The volume held by a household teaspoonful may vary, but a true teaspoonful equals 5 mL.
Table 4.7 Household Unit and Metric Unit Equivalents
| Volume | Weight |
|---|---|
1 tsp = 5 mL |
1 oz = 30 g† |
1 tbsp = 15 mL |
1 lb = 454 g |
1 fl oz = 30 mL* |
2.2 lb = 1 kg |
1 cup = 240 mL |
|
1 pt = 480 mL* |
|
1 qt = 960 mL |
|
1 gal = 3,840 mL* |
|
*There are actually 29.57 mL in 1 f l oz, but 30 mL is usually used. When packaging a pint, companies will typically include 473 mL, rather than the full 480 mL. Additionally, 1 gal is actually equivalent to 3,785 mL. †There are actually 28.34952 g in a household ounce; however, pharmacy personnel often round up to 30 g. |
|
Figure 4.3 Household Units for Volume and Their Metric Equivalents
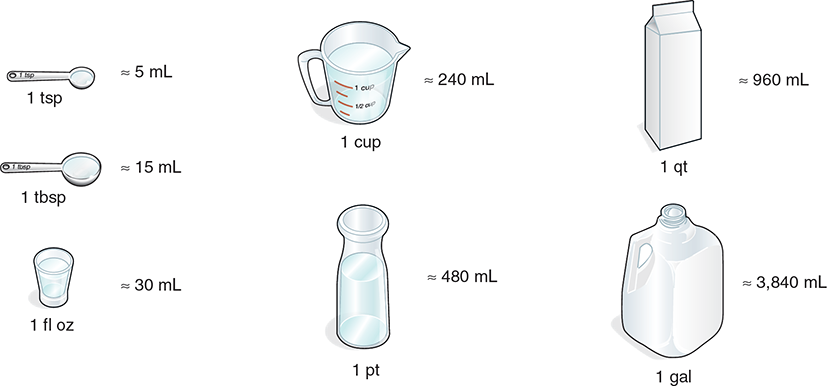
As indicated in Table 4.7 and Figure 4.3, it is common practice to round a household fluid ounce from 29.57 mL to 30 mL. When measuring this amount, this estimation is often appropriate because the volume differs by such a small amount. When measuring multiple fluid ounces that have been rounded up to 30 mL, however, the discrepancy becomes far more apparent. For example, if asked to measure a pint (16 fl oz), you would measure roughly 480 mL. This measurement becomes problematic because 29.57 mL multiplied by 16 is equal to only 473.12 mL, not 480 mL. Most pint stock medication containers are labeled 473 mL, yet pharmacies bill according to the estimation of 480 mL and measure out fluid ounces in 30 mL increments. For the purposes of this chapter, you will use the rounded 30 mL value for 1 fl oz and the rounded 480 mL value for 16 fl oz (or 1 pt).
 For Good Measure
For Good Measure
Using the household measurement equivalents given in this chapter, 1 pt equals 480 mL. However, pharmacy technicians should be aware that some pharmacies consider 473 mL to be equivalent to 1 pt.
The following examples show some typical conversion problems you must be able to solve when working in a pharmacy.
Example 4.5.1
You are to dispense 300 mL of morphine sulfate 100 mg/5 mL solution. The prescription states that the patient is to take 2 tsp two times daily. How many doses will the dispensed volume contain?

You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
To begin, convert the household measurement unit (2 tsp) to a metric measurement unit by using the conversion values in Table 4.7 and Figure 4.3. Place the unknown variable x over the known value (2 tsp) on the left side of the equation. Then place the conversion factor (1 tsp equals 5 mL) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
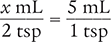
Then cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
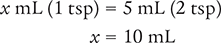
Next, determine the number of doses needed by setting up a proportion. Place the unknown variable x over the known value (300 mL) on the left side of the equation. Then place the conversion factor (1 dose equals 10 mL) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
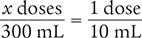
Then cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
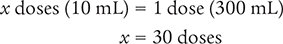
Dimensional Analysis Method
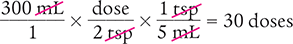
Answer: The dispensed volume will contain 30 doses.
Example 4.5.2
Using the medication and dosing instructions in Example 4.5.1, how many days will the 300 mL of morphine sulfate last?
You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
To begin, you know that the patient takes 1 dose twice daily and, as calculated in Example 4.5.1, there are 30 doses in the dispensed volume. Use this information to set up a proportion to determine how many days the 300 mL will last.
Place the unknown variable x over the known value (30 doses) on the left side of the equation. Then place the conversion factor (1 day equals 2 doses) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
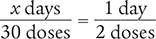
Then cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
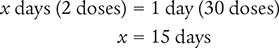
Dimensional Analysis Method
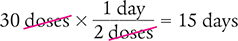
Answer: The 300 mL of morphine sulfate will last 15 days.
Example 4.5.3
A patient is to purchase a 12 fl oz bottle of antacid. The patient is to take 15 mL before each meal and at bedtime. How many doses does the bottle contain?
You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
To begin, convert the household measurement unit (12 fl oz) using the conversion values in Table 4.7 and Figure 4.3.
1 fl oz = 30 mL
Now, place the unknown variable x over the known value (12 fl oz) on the left side of the equation. Then place the conversion factor (1 fl oz equals 30 mL) on the right side of the equation. Note that the units in the numerators and in the denominators match.
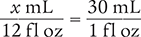
Then cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
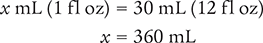
Next, determine the number of doses needed by setting up a proportion. Place the unknown variable x over the known value (360 mL) on the left side of the equation. Then place the conversion factor (1 dose equals 15 mL) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
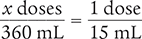
Then cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
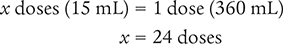
Dimensional Analysis Method
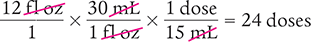
Answer: The bottle of antacid contains 24 doses.
Example 4.5.4
Use the medication and dosing instructions in Example 4.5.3 to solve the following problem. If the patient eats three times a day, how many days will the 12 fl oz bottle of antacid last?
To begin, you know that the patient is to take 1 dose with every meal and at bedtime. You also know that the patient eats three meals a day. Therefore, the patient will take four doses per day (one for each of three meals plus the bedtime dose).
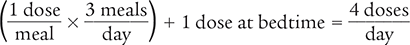
Then use your answer in Example 4.5.3 (24 doses) to determine how many days the bottle will last.
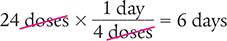
Answer: The 12 fl oz bottle of antacid will last 6 days.
Example 4.5.5
How many 2 tbsp doses are in 480 mL?
You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
To begin, convert the household measurement unit (2 tbsp) using the conversion values in Table 4.7 and Figure 4.3.
1 tbsp = 15 mL
Place the unknown variable x over the known value (2 tbsp) on the left side of the equation. Then place the conversion factor (1 tbsp equals 15 mL) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
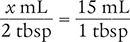
Then cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
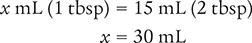
Next, determine the number of doses needed by setting up a proportion. Place the unknown variable x over the known value (480 mL) on the left side of the equation. Then place the conversion factor (1 dose equals 30 mL) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
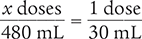
Then cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
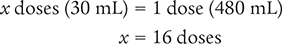
Dimensional Analysis Method
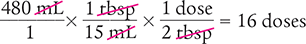
Answer: There are 16 doses (2 tbsp/dose) in 480 mL.
Example 4.5.6
A medication order indicates that a patient should take theophylline elixir. Theophylline elixir contains 80 mg/15 mL. One dose is 2 tbsp. How many milligrams are in one dose of the theophylline elixir?
 Name Exchange
Name Exchange
Theophylline elixir is also known by the brand name Elixophyllin, a combination of the words elixir and theophylline.

You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
To begin, convert the household measurement unit (2 tbsp) to a metric measurement unit by using the conversion values in Table 4.7 and Figure 4.3.
1 tbsp = 15 mL
Place the unknown variable x over the known value (2 tbsp) on the left side of the equation. Then place the conversion factor (1 tbsp equals 15 mL) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
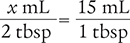
Then cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
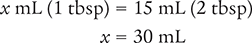
Next, determine the number of milligrams in one dose by setting up a proportion. Place the unknown variable x over the conversion value (30 mL) on the left side of the equation. Then place the concentration of the medication (80 mg/15 mL) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
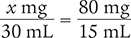
Then cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
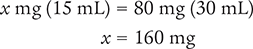
Dimensional Analysis Method
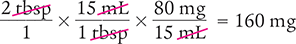
Answer: There are 160 mg in one dose of the theophylline elixir.
Like volumes, weights can be converted between household measurement units and metric measurement units. The most common conversions are between the household measurements of pounds and ounces and the metric measurements of kilograms and grams. These conversions are shown in Table 4.7.
Example 4.5.7
A medication order was received by the pharmacy for a 1.5 oz tube of ointment. How many grams of ointment are needed?
You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
To begin, convert the household measurement unit (1 oz) to a metric measurement unit by using the conversion value in Table 4.7.
1 oz = 30 g
Next, determine the number of grams by setting up a proportion. Place the unknown variable x over the known value (1.5 oz) on the left side of the equation. Then place the conversion factor (30 g/1 oz) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
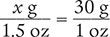
Then cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
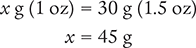
Dimensional Analysis Method
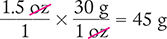
Answer: There are 45 g in a 1.5 oz tube of ointment.
Example 4.5.8
You have a 1 lb jar of ointment available. You are instructed to use this stock medication to fill smaller jars with 20 g of ointment each. How many jars can you fill?
You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
To begin, convert the household measurement unit (1 lb) to a metric measurement unit by using the conversion value in Table 4.7.
1 lb = 454 g
Next, determine the number of grams by setting up a proportion. Place the unknown variable x over the conversion factor (454 g) on the left side of the equation. Then place the known value (1 jar equals 20 g) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
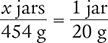
Then cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
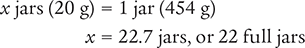
Dimensional Analysis Method
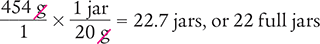
Answer: You can fill 22 full jars, with each jar containing 20 g of ointment.
In both solutions, there is 0.7 g of ointment remaining. You can determine how many grams of ointment are left over with the following calculation:
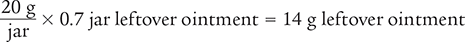
Converting Body Weight
Medications are sometimes dosed based on the weight of a patient. Increasingly, drug manufacturers are providing a recommended dose based on a specific dose in milligrams per kilogram (mg/kg) of a patient’s weight. Because most medications are dosed based on kilograms, you may need to convert a patient’s weight from pounds to kilograms before calculating the appropriate dose.
Example 4.5.9
A patient weighs 134 lb. What is this patient’s weight in kilograms?
You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
To begin, use the conversion value in Table 4.7.
1 kg = 2.2 lb
Next, determine the number of kilograms by setting up a proportion. Place the unknown variable x over the known value (134 lb) on the left side of the equation. Then place the conversion factor (1 kg equals 2.2 lb) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
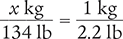
Then cross multiply, cancel similara units (like terms), and divide to solve for the unknown variable x.

Dimensional Analysis Method
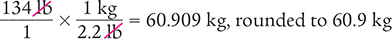
Answer: The patient’s weight is 60.909 kg, rounded to 60.9 kg.
Example 4.5.10
A patient weighs 76 lb. What is this patient’s weight in kilograms?
You can solve this problem by using the ratio-proportion method or by using the dimensional analysis method.
Ratio-Proportion Method
To begin, use the conversion value in Table 4.7.
1 kg = 2.2 lb
Next, determine the number of kilograms by setting up a proportion. Place the unknown variable x over the known value (76 lb) on the left side of the equation. Then place the conversion factor (1 kg equals 2.2 lb) on the right side of the equation. Note that the units in the numerators and the units in the denominators match.
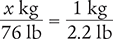
Then cross multiply, cancel similar units (like terms), and divide to solve for the unknown variable x.
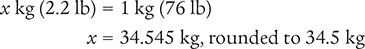
Dimensional Analysis Method

Answer: The patient’s weight is 34.545 kg, rounded to 34.5 kg.
Although it is important to understand the conversion using both the ratio-proportion and the dimensional analysis methods, a shorthand method for converting a patient’s weight from pounds to kilograms is to divide the patient’s weight by 2.2 lb/1 kg. Similarly, you can convert a patient’s weight from kilograms to pounds by multiplying the patient’s weight by 2.2 lb/1 kg.
Example 4.5.11
A patient weighs 58 kg. What is this patient’s weight in pounds?
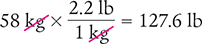
Answer: The patient’s weight is 127.6 lb.
To verify your answer, convert it from pounds back to kilograms.
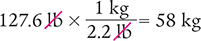
Example 4.5.12
A patient in the neonatal intensive care unit weighs 1,250 g. What is the patient’s weight in pounds?
To begin, convert grams to kilograms.
1,250 g = 1.25 kg
Then convert kilograms to pounds.
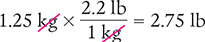
Answer: The patient’s weight is 2.75 lb.
To verify your answer, convert it from pounds back to kilograms.
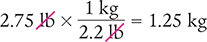
Example 4.5.13
A patient’s weight is recorded as 150 and does not include units. If the weight was reported in kilograms, how many pounds does the patient weigh?
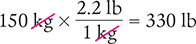
Answer: The patient’s weight is 330 lb.
 WORKPLACE WISDOM
WORKPLACE WISDOM
Many medications are dosed by weight (typically, milligrams per kilogram [mg/kg]). However, you may find a patient’s weight recorded without a unit of measurement, either by the patient, by the patient’s caregiver, or by a healthcare practitioner. You may also find the patient’s weight without a unit of measurement in the patient’s profile. If the unit of measurement is missing, it is imperative that you do not make assumptions regarding the unit and that you verify the patient’s weight and units. Mistaking pounds for kilograms can result in a patient receiving more than double the intended dose of medication. With some medications, a dose increase of that magnitude could result in harm or, possibly, death.
4.5 Problem Set
Convert the following volumes from the household measurement system to the metric measurement system. Round your answers to the nearest tenth when necessary.
3 tbsp = _____________ mL
1 fl oz = _____________ mL
2 fl oz = _____________ mL
3 fl oz = _____________ mL
4 fl oz = _____________ mL
5 fl oz = _____________ mL
6 fl oz = _____________ mL
7 fl oz = _____________ mL
8 fl oz = _____________ mL
12 fl oz = ____________ mL
16 fl oz = ____________ mL
Convert the given volumes between the household measurement and metric measurement systems. Round your answers to the nearest tenth when necessary.
80 mL = _____________ tbsp
6 fl oz = _____________ mL
90 mL = _____________ fl oz
800 mL = ____________ pt
53 mL = _____________ tsp
35 mL = _____________ tsp
10 L = _______________ gal
4 tbsp = _____________ mL
15 mL = _____________ tsp
720 mL = ____________ pt
30 tsp = _____________ mL
120 mL = ____________ fl oz
½ gal = ______________ mL
2 L = ________________ pt
Convert the following patient weights from pounds to kilograms. Round your answers to the nearest tenth when necessary.
3.5 lb = _____________ kg
14 lb = ______________ kg
42 lb = ______________ kg
97 lb = ______________ kg
112 lb = _____________ kg
165 lb = _____________ kg
178 lb = _____________ kg
247 lb = _____________ kg
Convert the following weights between the household and metric measurement systems. Round your answers to the nearest tenth when necessary.
2 oz = _____________ g
1.5 oz = ____________ g
8 oz = _____________ g
906 g = ____________ lb
30 g = _____________ lb
0.8 oz = ___________ g
Applications
In solving these problems, convert all quantities to the metric system. Round your answers to the nearest tenth when necessary.
How many 5 mL doses are in a 5 fl oz bottle?
How many 3 tsp doses are in 1 pt?
A dose of 1.5 fl oz is to be given three times daily. How many milliliters will be given in one day?
How many 1½ tsp doses are in an 8 fl oz bottle of cough syrup?
Use the following label to answer questions 44 and 45. Round your answers to the nearest tenth when necessary.

A prescription states that a patient is to take ½ tsp of furosemide oral solution daily. Using the furosemide label shown above, how many milligrams are in a dose?
Using the furosemide label shown above, how many days will a 4 fl oz bottle last a patient who is taking 20 mg daily?
Use the following label to answer questions 46–50. Round your answers to the nearest tenth when necessary.

A prescription states that a patient is to take 2.5 mL morphine sulfate oral solution four times daily as needed for pain. Using the provided label, calculate the equivalent dose measured in teaspoonfuls.
How many days will 320 mL of morphine sulfate oral solution last if a patient is taking 3 tsp daily?
A physician prescribes the following dose of medication for an adult patient: 2 tsp/68 kg/dose. How many doses would a 300 mL bottle contain for a patient who weighs 180 lb?
A physician prescribes the following dose of medication for a pediatric patient: 1 tsp/20 kg/dose. How many doses will a 4 fl oz bottle provide for a 52 lb patient?
A nurse practitioner writes the following prescription for a laxative: 2 tbsp/50 kg/dose. How many doses will a 12 fl oz bottle last for a patient who weighs 172 lb?
Self-check your work in Appendix A.