6.3 Figuring Ratios and Proportions

Ratios, proportions, and equations are perhaps the most frequently used mathematical equations in pharmacy practice. They are used in determining dosages and in compounding formulas

Ratios

A ratio is a way to demonstrate how two amounts of similar elements compare to each other in a whole. For example, if a beaker contains two parts water and three parts alcohol for a total of five parts, then the ratio of water to alcohol in the beaker can be expressed as the fractions $\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$ to $\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$ or as the ratio 2:3. The ratio is read not as an equation (2 ÷ 3), but as the expression “a ratio of two parts to three parts.”

Another common use of ratios is to express the number of parts of one substance contained in another substance of known parts. For example, suppose that there are 3 mL of an ophthalmic solution dissolved in a total 60 mL sterile saline solution. Thus it would be expressed as the ratio $\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$60$}\right.$, which reduces to $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$20$}\right.$. In other words, the ratio of the active ingredient to the sterile saline solution is 1 to 20, or 1 part in 20 parts.

Converting a Ratio to a Percent

To express a ratio as a percent, designate the first number of the ratio as the numerator and the second number as the denominator. Multiply the fraction by 100 ($\raisebox{1ex}{$100$}\!\left/ \!\raisebox{-1ex}{$1$}\right.$), and add a percent sign after the product.

${\displaystyle 5:1={\displaystyle \frac{5}{1}}\times {\displaystyle \frac{100}{1}}={\displaystyle \frac{5\times 100}{1}}=500\%}$

${\displaystyle 1:5={\displaystyle \frac{1}{5}}\times {\displaystyle \frac{100}{1}}={\displaystyle \frac{100}{5}}=100÷5=20\%}$

${\displaystyle 1:2={\displaystyle \frac{1}{2}}\times {\displaystyle \frac{100}{1}}={\displaystyle \frac{100}{2}}=100÷2=50\%}$

Converting a Percent to a Ratio

To convert a percent to a ratio, change it to a fraction by dividing it by 100 (and if needed, reduce the fraction to its lowest terms). Express the fraction as a ratio by making the numerator the first number and the denominator the second number.

${\displaystyle 2\%=2÷100={\displaystyle \frac{2}{100}};=2:100}$

Then simplify by dividing both numerator and denominator by 2 (the common factor).

${\displaystyle {\displaystyle \frac{1}{50}}=1:50}$

Now use the same process for the following conversions:

${\displaystyle 10\%=10÷100={\displaystyle \frac{1\cancel{0}}{10\cancel{0}}};\text{reduced to}{\displaystyle \frac{1}{10}}=1:10}$

${\displaystyle 75\%=75÷100={\displaystyle \frac{75}{100}};{\displaystyle \frac{75÷25}{100÷25}}\text{is reduced to}{\displaystyle \frac{3}{4}}=3:4}$

${\displaystyle 0.50\%=0.50÷100={\displaystyle \frac{.50}{100}};\text{increase by multiplying by}{\displaystyle \frac{2}{2}}\text{(which equals 1)}}$

${\displaystyle {\displaystyle \frac{1.00}{200}}=1:200}$

Equivalent Ratios

Two ratios that have the same value when simplified are different ways of saying the same ratio, such as $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ and $\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$8$}\right.$. They are called equivalent ratios. A pair of equivalent ratios together is called a proportion. The proportion can be expressed in three different ways:

${\displaystyle a/b=c/d\text{example}:{\displaystyle \frac{1}{2}}={\displaystyle \frac{4}{8}}}$

a:b = c:d example: 1:2 = 4:8

a:b :: c:d example: 1:2 :: 4:8

Because the ratios are equivalent, you can multiply the numerator of the first ratio with the denominator of the second ratio and then multiply the denominator of the first ratio with the numerator of the second ratio. The two resulting amounts should be equal.

The first and fourth numbers, or outside numbers, are called the extremes, and the second and third numbers, or inside numbers, are called the means.

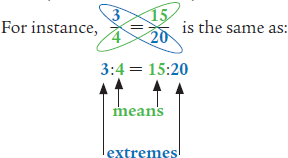
3 × 20 = 60 and 4 × 15 = 60; or 3 × 20 = 4 × 15

When you see it with the colors above, you can see why some people call this cross multiplication the “butterfly technique” or butterfly multiplying.

This cross multiplying can be stated as a rule:

${\displaystyle \text{If}{\displaystyle \frac{a}{b}}={\displaystyle \frac{c}{d}},\text{then}\mathbf{\text{a}}\times d=b\times c}$

the product of the extremes = the product of the means

As you have seen, the numerator of the first fraction times the denominator of the second is equal to the denominator of the first fraction times the numerator of the second. In other words, the multiplied extremes equal the multiplied means.

Here’s another example:

$\text{If}4:12=8:24,\text{ or }{\displaystyle \frac{\mathbf{4}}{\mathbf{12}}}={\displaystyle \frac{\mathbf{8}}{\mathbf{24}}};\text{ then }\mathbf{4}\times \mathbf{24}=\mathbf{12}\times \mathbf{8},\text{ or }\mathbf{96}\text{=}\mathbf{96}\mathrm{.}$

A Reciprocal Ratio

A reciprocal ratio is the inverse ratio, or the switching of the numerators with the denominators of both fractions. This gives you the mirrored ratio, which should also be equivalent, or proportional, though not equal to the originals.

${\displaystyle \text{If}1:20=3:60,\text{or}{\displaystyle \frac{\mathbf{1}}{\mathbf{20}}}={\displaystyle \frac{\mathbf{3}}{\mathbf{60}}};\text{then}\mathbf{1}\times \mathbf{60}=\mathbf{20}\times \mathbf{3}=60}$

${\displaystyle \text{Inversely}\text{if}20:1=60:3;\text{or}{\displaystyle \frac{\mathbf{20}}{\mathbf{1}}}={\displaystyle \frac{\mathbf{60}}{\mathbf{3}}};\text{then}\mathbf{20}\times \mathbf{3}=\mathbf{60}\times \mathbf{1}=60}$

These ratios are proportionally mirrored and also equivalent ratios though they are different in real value from the original ratios and fractions.

Another example:

${\displaystyle \text{If}3:2=9:6,\text{or}{\displaystyle \frac{\mathbf{3}}{\mathbf{2}}}={\displaystyle \frac{\mathbf{9}}{\mathbf{6}}},\text{then}\mathbf{3}\times \mathbf{6}=\mathbf{2}\times \mathbf{9}=18}$

then 2:3 will be an equivalent ratio to 6:9 though.

Using Equal Ratios and Proportional Equations of Extremes and Means

Pairs of equivalent ratios are useful in making conversions from one measurement system to another. Because they are proportionally equal, they can be used together with the butterfly technique to discover missing information and solve pharmaceutical conversions.

In mathematics, it is common to express unknown quantities by using letters from the lower end of the alphabet to represent them, especially x, y, and z.

Because x can get mixed up with the × for the multiplication sign, we will primarily use y and z. In our first example, the missing information has been named y, and you use the butterfly technique to figure out what y is.

${\displaystyle \text{Say}3:4=15:y\text{or}{\displaystyle \frac{\mathbf{3}}{\mathbf{4}}}={\displaystyle \frac{\mathbf{15}}{y}}.\text{Then}\mathbf{3}\times y=\mathbf{4}\times \mathbf{15.}\text{ This is }3y=60.}$

Then you just have to divide both sides of the equation by 3. Dividing by 3 is the same as multiplying by $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ as seen below:

${\displaystyle \left({\displaystyle \frac{1}{3}}\right)3y=60\left({\displaystyle \frac{1}{3}}\right)\text{or}{\displaystyle \frac{3y}{3}}={\displaystyle \frac{60}{3}}\text{to come up with}y=60÷3\text{or}y=20}$

Whenever you have an equation where you have a specified number of y that equals another number, as in the 3y = 60, all you have to do is take the number accompanying the y and divide each side of the equation by that number, as in: y = 60 ÷ 3.

Consider the equation 66y = 5,280. Solve for y by dividing each side of the equation by 66.

${\displaystyle {\displaystyle \frac{\cancel{66}y}{\cancel{66}}}={\displaystyle \frac{5,280}{66}}}$

Now we are left with:

${\displaystyle y={\displaystyle \frac{5,280}{66}}=80}$

Another way to approach this process is to multiply each equation by $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$66$}\right.$.

66y = 5,280

${\displaystyle {\displaystyle \frac{1}{\cancel{66}}}\times \cancel{66}y={\displaystyle \frac{1}{66}}\times 5,280}$

We arrive at the same conclusion utilizing this method:

${\displaystyle y={\displaystyle \frac{1}{66}}\times {\displaystyle \frac{5,280}{1}}={\displaystyle \frac{5,280}{66}}=80}$

Here’s another example of a proportion with missing numbers. You need to make 35 mL of a distilled water solution with a concentration of 2 g sodium chloride (salt) to each 7 mL of distilled water (or 2 g : 7 mL). How many grams of sodium chloride are needed?

${\displaystyle {\displaystyle \frac{y}{\mathbf{35}}}={\displaystyle \frac{\mathbf{2}}{\mathbf{7}}}}$

By the proportional rule, 2 × 35 = 7y, which equals 7y = 70. That means that y alone is equal to 70 divided by 7 or y = 70 ÷ 7 or y = 10. Another way to think of this is to divide both sides by 7.

${\displaystyle {\displaystyle \frac{\cancel{\mathbf{7}}y}{\cancel{\mathbf{7}}}}={\displaystyle \frac{70}{7}}}$

You can then cancel out the same multiplying factor on the top and the bottom of an equation and then divide 70 by 7 to equal 10. So this would leave y = 10 g of sodium chloride.

The following example shows how the ratio and proportion method is essential in both the community and hospital pharmacy settings for converting from one measurement system to another.