Pharmacy for Technicians: Seventh Edition

6.9 Advanced Calculations Used in Pharmacy Practice

As you will see, some pharmaceutical problems entail many complex steps or more advanced calculating concepts and skills. For instance, as a pharmacy technician, you may be asked to compound new solutions by combining measured amounts of different solutions of concentrated ingredients. This section will present some of these types of complex calculations. Other types of compounding require additional specialized knowledge or training and may be addressed in other chapters.

All require calculations practice, and this section is just an introductory overview to familiarize you with what you need to know before taking a course for further study. Because you need to understand both dimensional analysis and ratio and proportion, both techniques will be used for the advanced calculations, sometimes showing both options. This is not to confuse you, but to show that there are two options, and you can use one to double-check the other. Also, by knowing both, you understand the deeper principles of why they work.

Calculating Concentrations Based on Body Surface Area

For greater precision with particularly potent or toxic drugs, some dosages are based on body surface area instead of just weight. Body surface area (BSA) is a formulation of a patient’s weight and height expressed as meters squared (m²). (There are different medical formulas for arriving at the BSA.) Dosage prescriptions are then written as mg/m².

Many medications have a wide range for recommended dosages, because patients’ body shapes, sizes, bodily responses, and adverse reactions vary extensively, even among adults. That is why physicians prescribing cancer chemotherapy drugs particularly use BSA. Typical BSA averages used in US pharmacy are male adult, 1.9 m²; female adult, 1.6 m²; 12–13 years, 1.33 m²; 10 years, 1.14 m²; 9 years, 1.07 m²; 2 years, 0.5 m²; newborn, 0.25 m². As is clear, these are very general averages, not entailing differences in the age of the adults or the gender of the youth.

An equal proportion formula for calculating a specific dosage by BSA is this:

$\frac{y mg}{patient' {s m}^{2}} = \frac{dose mg}{1 m^{2}}$

Example 25

To treat the breast cancer of a patient with a BSA of 1.6 m2, the oncologist writes the following prescription for.

images Doxorubicin at a dose of 60 mg/m²

Doxorubicin is toxic to the blood cells and heart in excessive doses. What is the proper dose?

$\begin{matrix} y mg / 1.6 m^{2} = 60 mg / 1 m^{2} \\ \frac{y mg}{1.6 m^{2}} = \frac{60 mg}{1 m^{2}}; y mg = 60 mg \times 1.6 \\ y mg = 96 mg \end{matrix}$

The prescribed dose of doxorubicin is thus 96 mg.

Most pediatric prescribers favor those medications that have been particularly formulated for pediatric doses. However, there are times when a medical order comes in for calculating a child’s portion of an adult-use drug, so it is safer to prescribe using BSA instead of just weight. Remember to round down the dosage rather than up in pediatric patients for safety reasons.

Example 26

An adult patient with a BSA of 1.72 m2 requires a dose of 12 mg of a given medication. The same medication needs to be given to a child in a smaller pediatric-size dose. The child has a BSA of 0.60 m². If the pediatric dose were proportionally smaller than this adult patient’s dose, what would be this pediatric patient’s dosage? Round off the final answer.

As noted, children’s doses are often estimated with different proportional equations than adult dosages. However, if the child’s dose is to be directly proportional, it is possible to use a simple ratio and proportion equation to answer this question:

$\frac{child' s dose}{child' s BSA} = \frac{adult dose}{adult BSA}$

$\begin{matrix} \frac{y m g}{0.6 m^{2}} = \frac{12 m g}{1 . 72 m^{2}} \\ \begin{array}{l} \begin{matrix} y m g \times 1 . 72 = 0 . 6 \times 12 m g & 1.72 y mg = 7.2 mg & y mg = \frac{7.2 mg}{1.72 mg} \end{matrix} \\ y mg = 4.186 mg, rounded to 4 mg \end{array} \end{matrix}$

Because this dose is for a child, it is appropriate for safety reasons to round the dosage down to 4 mg rather than up to 4.2 mg.

Working with Dilutions

Medications may be diluted for several reasons. They are sometimes diluted prior to administration to infants, children, and older adults to meet dosage requirements. Medications may also be diluted so that they can be measured more accurately and easily. For example, volumes less than 0.1 mL are usually considered too small to measure accurately. Therefore, they must be diluted first. Many pharmacies have a policy for tuberculin syringes that the injection should have a volume greater than 0.1 mL and less than 1 mL.

Practice Tip

Many medical scientists are finding that different age groups, especially in childhood ages, have different metabolism rates and organ effects. Some pediatric practices call for calculating dosages through additional formulas. That is why pediatric compounding is becoming a specialty for pharmacists and technicians.

The pharmacist usually calculates the dilution amounts. However, the technicians double-check the answers to ensure accuracy. If there is a discrepancy, the technician brings the different answer to the pharmacist for the pharmacist to recalculate.

The following example demonstrates the method for solving typical dilution problems. The first step is to determine the sufficient volume of the final product needed to attain the prescribed drug strength. One must first establish the ratio of diluted solution strength to the desired strength. The second step is to determine the amount of diluent needed by subtracting the original amount of the solution from the total volume of the final diluted product. (Both of these small volumes are approximate because they depend on the calibration and accuracy of the measuring devices used.)

Although the second step uses subtraction to determine the amount of diluent needed, the diluent will actually be added to the original concentration. The abbreviation QS for “sufficient quantity” is used to describe the process of adding enough of the ingredient to reach the desired volume for sufficient active drug strength.

Example 27

Dexamethasone sodium phosphate is available as a 4 mg/mL sterile preparation for injection. An infant is to receive 0.35 mg. The volume needed would be a miniscule 0.08 mL of the 4 mg/mL solution, which is very difficult to accurately measure. Prepare a dilution in a syringe or vial for a final concentration of 1 mg/mL.

For Good Measure

An injected dose in a tuberculin syringe generally measures a volume greater than 0.1 mL but less than 1 mL.

How much sterile water diluent will you need to add? How much of the newly diluted solution will you need to draw into the syringe (or vial) for an accurate measurement of the 0.35 mg prescription?

Step 1	Determine the volume needed (in milliliters) of the final diluted product that will be mixed in a vial or syringe. The strength of the dexamethasone is currently 4 mg/mL, which means that every 1 mL has 4 mg of the drug. You want a final concentration of 1 mg/mL, so to have 4 mg of the medication at a 1:1 ratio, you will need to have 4 mg/4 mL. (This is a common pharmaceutical dilution concentration goal, since it makes it easy to determine the volume needed because of the 1:1 ratio.) This means that you will need 4 mL total volume of the final product, as shown below, using the ratio and proportion method. Prescribed drug strength Desired concentration $\frac{y mL}{4 mg} = \frac{1 mL}{1 mg}$ $y mL = \frac{4 mg \times 1 mL}{1 mg} = 4 mL$
Step 2	Take the required volume (4 mL) and subtract from it the volume (1 mL) of the original 4 mg/mL prescribed solution to determine the volume of sterile water needed. 4 mL – 1 mL = 3 mL Therefore, an additional 3 mL of sterile water is needed to dilute the original 1 mL of the preparation to arrive at a final concentration of 1 mg/mL.
Step 3	Set up a dimension analysis equation to determine the volume of medication to be prepared from the diluted medication. $y mL = 0.35 mg \times \frac{1 mL}{1 mg}$ y mL = 0.35 mL
This volume of 0.35 mL can be more accurately compared to original 0.08 mL, yet the same 0.35 mg drug strength will be administered.

For Good Measure

When calculating dilutions for sterile compounding, check for the amount of "overfill" on the label. Manufacturers of IV solutions overfill them by a certain percentage to allow for evaporation. This will affect your dilutions. Different cleanrooms have different ways of handling overfill. This will be addressed in Chapter 13.

images IN THE REAL WORLD

In the neonatal intensive care unit of a major hospital, a microdilution of insulin was ordered for a newborn. The desired insulin was to be 1 mL per unit. The insulin required two dilutions to get into micro-dilutions, moving from:

$\frac{100 units}{1 mL} + dilution = \frac{10 units}{1 mL} + dilution = \frac{1 unit}{1 mL}$

The technician successfully did the first dilution but unfortunately either stopped there or mixed up the dilutions and drew the wrong solution for the patient’s final dose. The pharmacist did not catch the error, and the patient received a tenfold dose of insulin. This resulted in serious complications for the infant.

Calculating Percent Weight-in-Volume for Dilution Levels

Injectable drugs and IV solutions are available in concentrations expressed in various percentages, and many IV solutions may be medically ordered as a percentage of active ingredient weight based on solution volume. Weight-in-volume is usually expressed as grams of the active ingredient per 100 milliliters of solution, as expressed by the following formula:

1% = 1 g per 100 mL

Percent weight-in-volume is most commonly used in pharmacy practice. Premade preservative-free lidocaine, for instance, is available in 1% and 2% concentrations for intravenous use. To calculate dilution levels, you need to convert from percentages to fractions and from grams to milligrams of actual ingredient in a concentration. For instance:

Step 1

Convert from grams to milligrams.

$1 g \times \frac{1000 mg}{1 g} = 1, 000 mg$

Step 2

Simplify the proportion, eliminating powers of ten or equal numbers of zeros at the end of the numerator and the denominator.

$\frac{1, 000 mg}{100 mL} = 10 mg per 1 mL$

Example 28

How much potassium chloride (in grams) is needed to prepare a 2% solution in 1 Liter of normal saline? Both the ratio and proportion method and dimensional analysis will be shown.

Using the ratio and proportion method:

Step 1

Rewrite 2% potassium chloride with the units of grams per milliliter. By definition, 2% potassium chloride is 2 g of potassium chloride per 100 mL of solution. Written as a fraction,

$2 % potassium chloride = \frac{2 g potassium chloride}{100 mL solution}$

Step 2

To ensure the units in the numerator and denominator of both proportions are the same, convert 1 L to milliliters.

1 liter = 1,000 mL

Step 3

Set up the two equivalent ratios and solve for the unknown grams of potassium chloride and solve for the unknown grams per potassium chloride.

$\frac{y g potassium chloride}{1, 000 mL solution} = \frac{2 g potassium chloride}{100 mL solution}$

$y g potassium chloride = 2 g potassium chloride \times \frac{1, 000 mL}{100 mL}$

y g potassium chloride = 20 g potassium chloride

Dimensional analysis method:

$1, 000 mL solution \times \frac{2 g potassium chloride}{100 mL solution} = 20 g$

Mixing Dry Powders and Dilution Rates

At times, you will need to do calculations with dry powdered forms of active ingredients. For example, parenteral products are often reconstituted by adding a diluent to a lyophilized or freeze-dried powder to prepare an IV solution. The product is commercially manufactured in powder form because of the instability of the drug in a solution over a long period. The active ingredient (the powder) is expressed in terms of weight, but it also occupies a certain amount of space, or volume. This space is referred to as powder volume (pv). It is equal to the difference between the total volume (tv) of the final product and the volume of the diluting ingredient, or the diluent volume (dv), as expressed in the following equations:

Name Exchange

Total volume (tv) can also be known as final volume (fv); diluent (dv) is also abbreviated (Dil).

total volume = powder volume + diluent volume [tv = pv + dv]

powder volume = total volume – diluent volume [pv = tv – dv]

diluent volume = total volume – powder volume [dv = tv – pv]

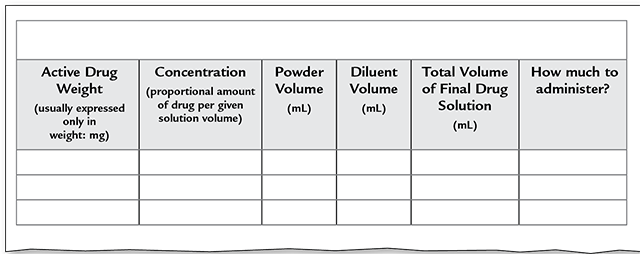
Trying to keep the different aspects involved in a powder-reconstitution equation straight can be very confusing. It is important to break the information into pieces and use the form in Figure 6.4 to help you do the calculations correctly.

The weight of the powder drug is the amount that shall be added for the solution concentration. The space that the active drug will take up in the final solution is what is not taken up by the diluent. So if you consider the final drug as a couple’s closet, the powder volume is the amount of room one partner gets to use versus the other (and that it is rarely equal!). The space each takes up is different from the weight of the shoes and clothes stored in that part of the closet.

Figure 6.4 Drug Dilution Calculation Form

Example 29

A dry powder antibiotic must be reconstituted for use. The label states that the dry powder occupies 0.5 mL. Using the formula provided, determine the diluent volume (with the amount of solvent added). You are given the total volume for three different examples with the same powder volume but different diluent volumes and resulting concentrations.

tv – pv = dv

Total Volume			Powder Volume	Diluent
(1)	2 mL	–	0.5 mL	= 1.5 mL
(2)	5 mL	–	0.5 mL	= 4.5 mL
(3)	10 mL	–	0.5 mL	= 9.5 mL

Example 30

You are to reconstitute 1 g of dry powder. The label states that you are to add 9.3 mL of diluent to make a final solution of 100 mg/mL. What is the powder volume?

If the patient’s medical order is for 50 mg of the drug, how much must be drawn from the vial into the syringe?

Step 1

Calculate the total volume using the ratio and proportion method. The strength of the final solution must be 100 mg/mL, so you need to convert the grams of active ingredient into milligrams. Since you start with 1 g = 1,000 mg of powder, for a total volume y mL of the solution, it will have a strength of 1,000 mg/y mL.

$\frac{100 mg}{1 mL} = \frac{1, 000 mg}{y mL}$

100 mg × y mL = 1 mL × 1,000 mg

$y mL= \frac{1, 000 mg \times 1 mL}{100 mg} = 10 mL$

Step 2

Using the calculated total volume of the final product and the given diluent volume, calculate the powder volume.

tv − dv = pv

10 mL − 9.3 mL = 0.7 mL

Step 3

You have a final drug solution of 100 mg per 1 mL, or 1 mL containing 100 mg of the drug. You must have only 50 mg in the syringe. So how much drug volume should be put into the syringe?

$50 mg \times \frac{1 mL}{100 mg} = \frac{50 mL}{100} = 0.5 mL$

So now you can finish filling in the chart, and load the syringe with 0.5 mL of the drug solution.

Name Exchange

Because of the grid used in the alligation alternate method, it has been nicknamed “Tic-Tac-Toe Math.”

Using Alligation to Combine More than One Concentration Level

Physicians often prescribe concentrations of medications that are not commercially available, and these prescriptions must be compounded, or prepared by an integration of ingredients, at the pharmacy. When a prescribed concentration is not commercially available, it may be necessary to combine two products of different concentrated strengths to reach the prescribed concentration. This process is called an alligation. The resulting concentration will be greater than the weaker strength but less than the stronger strength.

Safety Alert

Pharmacy technicians should always have the pharmacist verify their calculations and double-check those of the pharmacist.

For example, a 1% and a 5% hydrocortisone ointment may be combined to provide a 3% ointment. An alligation calculation method is used when the two quantities to be combined are both relatively large. (To learn more about the techniques for combining topical creams of different strengths, refer to Chapter 10.)

Cream being mixed with spatula

When the desired concentration of a cream (ointment or solution) is not available, the technician can use alligation to calculate how much cream of each concentration should be mixed together to compound the prescription.

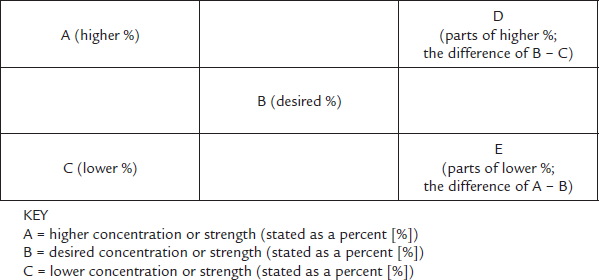
There are two alligation methods: alligation medial and alligation alternate. The amount of each stock product ingredient to be added together is calculated by using what is known as the alligation alternate method. It is a very visual form of calculation, where you create a kind of tic-tac-toe grid to calculate the different percentages.

The first step is to make the familiar tic-tac-toe grid and place the highest ingredient percentage concentration in the top left-hand corner box. The lowest concentration is placed in the lower left corner box. Your target concentration, logically, is placed in the middle box. Then you need to figure out the “steps” in between each corner amount and the middle. You do this by subtracting the middle amount from the top left number (i.e., the smaller from the larger) and placing the answer in the lower right corner. This makes a diagonal line going from top to bottom (see Figure 6.5).

Now subtract the lower left number from the center number (i.e., the smaller from the larger) and put it at the upper right corner. This gives you another diagonal line going from bottom to top.

At this point, you have two percentages in the first column of the grid. Across from them in the facing corners, you have the number of parts of that percentage needed for the full solution. You will apply the number of parts to the percentage in each row going across. Then you add up the number of parts (or proportional items) you need to create your whole.

Once you know the total parts, you can divide that into the desired volume of the completed product to find out how much each part is worth, or its volume. Once you know that, then you can put it together like a recipe, mixing in the correct number of parts of each. It will make more sense when you follow the examples below.

Figure 6.5 Alligation Grid

The tic-tac-toe grid pattern of alligation helps one calculate how many parts of each strength are needed. The reason it crosses from top to bottom and bottom to top that you always want fewer parts of the high strength to go with more parts of the low strength to balance out to the mid strength.

Example 31

Prepare 250 mL of dextrose 7.5% weight-in-volume (w/v)—or 250 mL of D7.5W. Combine the stock products of dextrose 5% (D₅W) w/v and dextrose 50% (D₅₀W) w/v. How many milliliters of each will be needed?

Step 1	Identify the variables by determining the component concentrations. B% is the desired concentration. The higher concentration (A%) and lower concentration (C%) are determined by the stock IV base solution strengths on hand in your pharmacy. In this case, the desired concentration is 7.5%, the higher concentration is 50%, and the lower concentration is 5%.
Step 2	Using the alligation grid from Figure 6.5, fill in the concentration strengths (given as percentages) in the key section below the tic-tac-toe grid. Place the same strengths in their designated squares on the grid.

A (higher %)

D (parts of higher %; the difference of B − C)

B (desired %)

7.5

C (lower %)

E (parts of lower %; the difference of A − B)

KEY

A% =50

B% = 7.5

C% = 5

D (Parts of 50% solution)

E (Parts of 5% solution)

Step 3

Determine the number of parts of each component (higher % and lower %).

To find the value of D in the upper right-hand square, set up the equation B−C = D.

Fill in the values for B and C (found in Step 2) in the equation, as shown below:

7.5−5 = D

D = 2.5 (or the number of parts of 50% dextrose)

Record the number 2.5 in the key and in the upper right-hand square.
To find the value of E in the lower right-hand square, set up the equation A−B = E.

Then fill in the values for A and B (found in Step 2) in the equation, as shown below:

50 – 7.5 = E

E = 42.5 (or the number of parts of 5% dextrose)

Record the number 42.5 in the key and in the lower right-hand square.

Check that your completed grid now matches the grid shown below:

A (higher %) 50		D (parts of higher %; the difference of B − C) 2.5
	B (desired %) 7.5
C (lower %) 5		E (parts of lower %; the difference of A − B) 42.5

KEY

A% = 50

B% = 7.5

C% = 5

D (Parts of 50% solution) = 2.5

E (Parts of 5% solution) = 42.5

Step 4	Set up a ratio using the values of D and E as shown in the right-hand column of your completed grid. $\frac{D}{E} = \frac{2.5}{42.5}$
This ratio indicates that to prepare the desired concentration (in this case, a D_7.5 W solution), dextrose 50% (D₅₀W) and dextrose 5% (D₅W) must be mixed in a 2.5:42.5 ratio: 2.5 parts of D50% and 42.5 parts of D5%.
Step 5	Using the ratio from Step 4, add D and E to obtain the total number of E (Parts of 5% solution) = 42.5 parts (tp). D + E = tp 2.5 + 42.5 = tp 45 = tp
Step 6	Determine the volume of each component. Determine the volume of dextrose 50% (D₅₀W) needed: total volume (tv) of desired concentration = 250 mL parts of D₅₀W (D) = 2.5 total number of parts (tp) = 45 $\frac{D}{tp} = \frac{x}{tv}$ $\frac{2.5}{45} = \frac{x}{250 mL}$ x = 13.9 mL of D₅₀W Determine the volume of dextrose 5% (D₅W) needed: total volume (tv) of desired concentration = 250 mL parts of D₅W (E) = 42.5 total number of parts (tp) = 45 $\frac{E}{tp} = \frac{x}{tv}$ $\frac{42.5}{45} = \frac{x}{250 mL}$ x = 236.1 mL of D₅W Therefore, to make D7.5% (D7.5W) 250 mL, mix 13.9 mL of dextrose 50% (D₅₀W) with 236.1 mL of dextrose 5% (D₅W).
Step 7	Verify your answer. The volume of each component (determined in Steps 6a and 6b) when added together should equal the total volume of the desired concentration. volume of D₅₀W = 13.9 mL volume of D₅W = 236.1 mL 13.9 mL + 236.1 mL = 250 mL

Example 32

You are instructed to make 454 g of 3% zinc oxide cream. You have in stock 10% and 1% zinc oxide cream. How much of each percent will you use?

Step 1

Identify the variables by determining the component concentrations. The desired concentration (B%) is what you are asked to prepare. The higher concentration (A%) and lower concentration (C%) are determined by the stock strengths on hand in your pharmacy. In this case, the desired concentration is 3%, the higher concentration is 10%, and the lower concentration is 1%.

Step 2

Using the alligation grid from Figure 6.5, fill in the concentration strengths (given as percentages) in the key section below the tic-tac-toe grid. Place the same strengths in their designated squares on the grid.

A (higher %) 10		D (parts of higher %; the difference of B − C)
	B (desired %) 3
C (lower %) 1		E (parts of lower %; the difference of A − B)

KEY

A% = 10

B% = 3

C% = 1

D (parts of 10% cream)

E (parts of 1% cream)

Step 3

Determine the number of parts of each component (higher % and lower %).

To find the value of D in the upper right-hand square, set up the equation B – C = D. Fill in the values for B and C (found in Step 2) in the equation, as shown below:

3 – 1 = D

D = 2 (or the number of parts of 10% zinc oxide cream)

Record the number 2 in the key and in the upper right-hand square.
To find the value of E in the lower right-hand square, set up the equation A – B = E.

Fill in the values for A and B (found in Step 2) in the equation, as shown below:

10 – 3 = E

E = 7 (or the number of parts of 1% zinc oxide cream)

Record the number 7 in the key and in the lower right-hand square.

Check that your completed grid now matches the grid shown below:

A (parts of higher %; the difference of B − C) 10		D (parts of higher %; the difference of B − C) 2
	B (desired %) 3
C (lower %) 1		E (parts of lower %; the difference of A − B) 7

KEY

A% = 10

B% = 3

C% = 1

D (parts of 10% cream) = 2

E (parts of 1% cream) = 7

Step 4

Set up a ratio using the values of D and E as shown in the right-hand column of your completed grid.

$\frac{D}{E} = \frac{2}{7}$

This ratio indicates that to prepare the desired concentration (in this case, a 3% cream), zinc oxide cream 10% and zinc oxide cream 1% must be mixed in a 2:7 ratio: 2 parts of zinc oxide cream 10% and 7 parts of zinc oxide cream 1%.

Step 5

Using the ratio from Step 4, add D and E to obtain the total number of parts (tp).

D + E = tp

2 + 7 = tp

9 = tp

Step 6

Determine the volume of each component.

Determine the amount of zinc oxide cream 10% needed.

total amount (ta) of desired concentration = 454 g

parts of zinc oxide cream 10% (D) = 2

total number of parts (tp) = 9

$\frac{D}{tp} = \frac{x}{ta}$

$\frac{2}{9} = \frac{x}{454 g}$

x = 100.9 g of zinc oxide cream 10%
Determine the amount of zinc oxide cream 1% needed.

total amount (ta) of desired concentration = 454 g

parts of zinc oxide cream 1% (E) = 7

total number of parts (tp) = 9

$\frac{E}{tp} = \frac{x}{ta}$

$\frac{7}{9} = \frac{x}{454 g}$

x = 353.1 g of zinc oxide cream 1%

Therefore, to make zinc oxide cream 3% 454 g, mix 100.9 g of zinc oxide cream 10% with 353.1 g of zinc oxide cream 1%.

Step 7

Verify your answer. The volume of each component (determined in Steps 6a and 6b) when added together should equal the total volume of the desired concentration.

amount of zinc oxide cream 10% = 100.9 g

amount of zinc oxide cream 1% = 353.1

100.9 g + 353.1 g = 454 g

Calculating Specific Gravity

In precision compounding, it is important to understand that each substance has its own specific gravity due to its particular density or molecular structure. This determines how well various elements mix in solutions, suspensions, and emulsions. For instance, oil is less dense than water or has a lower specific gravity, so oil floats.

Specific gravity is the weight of a substance compared in a ratio to the standard weight of an equal volume of water when both are the same temperature at sea level. Water is the standard because 1 mL of water at sea level and room temperature weighs approximately 1 gram (it is 1.0 gram precisely at 39.2°F/4.0°C).

Water and oil have different specific gravity ratings.

1 mL volume of water = 1 g weight of water

Specific gravity of water = 1.0

Specific gravity measurements are always calculated from the weight of the substance in grams compared to an equal volume of water in grams. The resulting number is a rating against the standard of 1. The formula for a specific gravity rating is as follows:

$specific gravity rating = \frac{weight of a substance (g)}{weight of an equal volume of water (mL)}$

$or mL = \frac{weight (g)}{specific gravity}$

or g = mL × specific gravity

The formulas above can be used to calculate the unknown value of specific gravity, or the ratio and proportion method can be utilized. When the specific gravity is known, certain assumptions can be made regarding the physical properties of a liquid. Solutions that are thick (or viscous) often have specific gravities higher than one (1), meaning that they are heavier than water. Solutions that contain volatile chemicals (or something prone to quick evaporation, such as alcohol) often have a specific gravity lower than one (1), meaning that they are lighter or less dense than water. If the specific gravity is known, you can determine the weight of a liquid volume by reversing the equations or by using equal proportion equations (see Table 6.11).

Table 6.11 Specific Gravity Ratings for Different Liquids

Liquid	≈ Specific Gravity Rating at Sea Level
Alcohol—isopropyl	0.79
Ammonia	0.662
Beer	1.01
Butane	0.584
Corn oil	0.924
Glucose	1.35
Mercury	13.6
Molasses (blackstrap)	1.49
Seawater	1.02

Example 33

If the weight of 100 mL of dextrose solution is 117 g, what is the specific gravity of the dextrose solution?

$specific gravity rating = \frac{weight of a substance}{weight of an equal volume of water}$

$y = \frac{117 g}{100 mL} = 1.17. This solution is heavier than water .$

Example 34

If 500 mL of glycerin weighs 275 g, what is the specific gravity?

$y = \frac{275 g}{500 mL} = 0.55. This solution is lighter than water .$

Example 35

If a liquid has a specific gravity of 0.85, how much does 125 mL of it weigh?

Because the specific gravity of the liquid is 0.85,

$0.85 = \frac{85 g}{100 mL}$

Now, use the ratio and proportion method to find the weight of 125 mL.

$\frac{y g}{125 mL} = \frac{85 g}{100 mL}$

$100 y g = 125 \times 85 g y g = \frac{10, 625 g}{100} = 106.26 g$

So, 125 mL of the liquid weighs 106.25 g.

Calculating Milliequivalents

This section is challenging and may require some basic chemistry knowledge as well as mathematical prowess. It is designed for pharmacy technicians who will be compounding sterile products in a hospital or home healthcare IV facility or nonsterile products in a community pharmacy setting. Even so, a basic understanding of electrolytes and milliequivalents (mEq) will enhance the expertise of any pharmacy technician and may minimize calculation errors. Because of this, technician programs must teach these calculations, and these calculations could be included in the Pharmacy Technician Certification Board (PTCB) certification examination.

Calculating Atomic and Molecular Weights

Most electrolyte solutions in the hospital pharmacy are measured by milliequivalents (mEq), which are related to molecular weight. Molecular weights are calculated using the established atomic weight of each of the common chemical elements. You may recall from high school chemistry class the periodic table of elements on the wall. On it was listed the atomic weight of each element—the weight of a single atom as compared to the weight of one atom of hydrogen, which is the standard. For instance, the atomic weight of H (hydrogen) is 1; C (carbon) is 12.01 rounded off to 12; and Na (sodium) is 22.9898, rounded off to 23.

The molecular weight of a compound is the sum of the atomic weights of all the atoms in one molecule of the compound. The molecular weight of sodium bicarbonate (NaHCO₃) is 23 +1 + 12 + 48 (see Table 6.12).

Table 6.12 Valences and Atomic Weights of Common Elements

Element	Valence	Atomic Weight	Rounded-off Value
Hydrogen (H)	1	1.008 g	1 g
Carbon (C)	2, 4	12.011 g	12 g
Nitrogen (N)	3, 5	14.007 g	14 g
Oxygen (O)	2	15.999 g	16 g
Sodium (Na)	1	22.9898 g	23 g
Magnesium (Mg)	2	24.305 g	24.31g
Sulfur (S)	2, 4, 6	32.065 g	32.1 g
Chlorine (Cl)	1, 3, 5, 7	35.453 g	35.5 g
Potassium (K)	1	39.102 g	39.1 g
Calcium (Ca)	2	40.08 g	40.1 g

A mole (mol) is a unit of measurement based on the number of particles in a given substance. The mass of one mole of a substance is its molecular weight expressed in grams. The number of grams in one mole differs between substances. For example, a mole of potassium (K+) is 39.10 grams and a mole of chlorine (Cl-) is 35.45 grams. A millimole (mmol) is one-thousandth of a mole, or the molecular weight expressed in milligrams. One millimole of potassium (K+) is 39.19 mg and one millimole of chlorine (Cl-) is 35.45 mg.

atomic weight of sodium (23 g) + atomic weight of chlorine (35.5 g) = 58.5 g

Compounds are also measured in moles. For example, 1 mole of salt (or sodium chloride, NaCl) would equal the total of the atomic weights of the two components in grams, which is as follows:

As another example, 1 mole of calcium chloride (CaCl₂) would be:

1 mole of calcium (40) + 2 moles of chlorine (71) = approximately 111 g

As stated earlier, 1 mM is the molecular weight of one millimole expressed in milligrams.

1 mM of sodium chloride = 58.5 mg

1 mM of calcium chloride = 111 mg

Understanding the Dissolving Capacity of Solutes

Besides atomic weights, each element is described by its ability to form bonds with other elements. In chemistry, the valence is a positive or negative number that represents its rated capacity to combine with other atomic substances to form a molecule of a stable compound. The valence is based on the number and typical activities of the outer electrons of the element to bind or repel electrons in other atoms. An element can exist in various forms, and the valence can vary depending on the molecular form and compound. In pharmacy, the valence is used to determine the number of grams of solute that have the capacity to fully dissolve in 1 mL of solution.

Table 6.12 lists the atomic weights and valences of common elements. For pharmaceutical calculations, atomic weights are usually rounded to the nearest tenth, as shown in the fourth column of the table.

An equivalent (Eq) weight is a unit that takes into account both moles and valence. In pharmacy, you are often trying to find out the equivalent weight of the amount of solute substance that is fully able to dissolve in 1 mL. The equivalent (Eq) weight is equal to 1 mole of the molecule divided by its valence, or the number of grams of solute that could dissolve in 1 mL of solution as shown in the following formula:

$equivalent (Eq) weight = \frac{1 M's molecular weight (in grams)}{valence}$

$Eq = \frac{1 M g}{valence}$

A milliequivalent (mEq) weight is equal to 1 mM divided by its valence.

$milliequivalent (mEq) weight = \frac{1 mM's molecular weight (in milligrams)}{valence}$

$mEq = \frac{1 mM (in mg)}{valence}$

Further, 1 Eq equals 1,000 mEq.

Determining the Milliequivalents of Compounds

The first step in determining the number of milliequivalents of a compound is to identify the formula of the compound. The next step is to separate the formula into the atomic weight of each element. The atomic weight of an individual atom of each element is then multiplied by the number of those atoms. Then the products are added together, and that sum is substituted into the formula for atomic weight.

Example 36

The molecular weight of magnesium sulfate (Mg + SO₄) is 120 g. This comes from Mg + S + O₄ = 24.306 g + 32.064 g + 15.999 g (× 4) = 120 g. Its valence is 2. How many milligrams does 1 mEq of magnesium sulfate weigh?

$1 mEq = \frac{120 mg}{2} = 60 mg$

Example 37

Magnesium has an atomic weight for a mole of 24 g. What is the weight of 1 mM?

To solve this problem, you must recall metric prefixes. The prefix milli- means 1,000. Therefore, 1 M = 1,000 mM. Now we will use dimensional analysis to calculate the number of grams in 1 mM.

$\frac{24 g}{1 M} \times \frac{1 M}{1, 000 mM} = 0.024 g per mM = 24 mg per mM$

Converting between Milligrams and Milliequivalents

To convert back and forth between the weight of a substance in milligrams and its dissolving weight in milliequivalents, use the following formula:

$number of milliequivalents = \frac{weight of substance (in milligrams)}{milliequivalent weight}$

This equation will be demonstrated in the following example.

Example 38

Sodium has an atomic weight of 23 mg and a valence of 1. How many milliequivalents are in 92 mg of sodium?

Step 1

Determine the weight of 1 milliequivalent of sodium by dividing the molecular weight (from the atomic weight) by the valence.

$1 mEq = \frac{molecular weight}{valence} = \frac{23 mg}{1} = 23 mg$

Step 2

Determine the number of milliequivalents in 92 mg of sodium.

$y mEq = \frac{weight of sodium in solution}{weight of mEq of sodum} = \frac{92 mg}{23 mg} = 4 mEq$

Measuring Electrolytes

Many IV fluids used in hospital pharmacy practice contain dissolved mineral salts; such a fluid is known as an electrolyte solution. These fluids are so named because they conduct an electrical charge through the solution when connected to electrodes. For example, the compound potassium chloride (abbreviated KCl) breaks down to K+ and Cl— ions in solution.

Milliequivalents (and sometimes millimoles) are used to measure electrolytes in the bloodstream and/or in an IV preparation. For these you need to figure out the milliequivalents able to dissolve in the solution to reach the proper concentration.

Example 39

You are requested to make a sterile preparation in the IV room by adding 44 mEq of sodium chloride (NaCl) to an IV bag. Sodium chloride is available as a 4 mEq/mL solution. How many milliliters will you need to add to the IV bag?

Set up a ratio and proportion, comparing the solution you will need to create to the available solution, and solve for the unknown y.

$\frac{4 mEq}{1 mL} = \frac{44 mEq}{y mL}$

y mL × 4 = 44 × 1 mL

$y mL = \frac{44 \times 1 mL}{4}$

y mL = 11 mL

You can also solve this problem using dimensional analysis.

Determining IV Administration Flow Rates

In sterile compounding, pharmacy technicians are often called upon to calculate IV drip rates, drop factors, and the IV quantity for the prescribed period based on infusion rates prescribed by the physician. Because these rates are in part determined by the size and nature of the tubing, these calculations will be addressed in Chapter 13 after the IV tubing and sets have been described. The calculation of overfill volumes is also handled in Chapter 13 on sterile and hazardous compounding procedures.

Beyond-Use Dating

When compounding together two different manufactured drug products, each comes with its own properties of stability, or ability to maintain its potency and essential properties and active ingredients over time in proper storage and temperature conditions. Stability includes physical properties (appearance, taste, uniformity, dissolution, and suspendability) and chemical properties (potency). Based on this, an expiration date, or date of last recommended use, has been assigned by the manufacturer. Each ingredient in the alligated or compounded product has a different expiration date.

Practice Tip

A beyond-use date is a term that applies to both sterile and nonsterile compounded preparations, whereas an expiration date is a term that applies to manufactured products.

From these dates, the pharmacist needs to calculate a date for last recommended use, called beyond-use date (BUD) for the product, and the technician serves to double-check the calculation. The pharmacist considers the expiration dates and the stability of the new compound’s ingredients and then calculates a BUD from them.

The US Pharmacopeial Convention has established beyond-use-dating guidelines for alligation and compounded nonsterile drug products in USP General Chapter <795> (rev. 2019) and for sterile products in USP <797>. Since nonsterile and sterile products have different BUD dating guidelines, the way to calculate them will be addressed in Chapter 10 and Chapter 13.