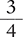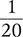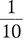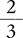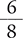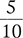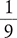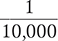2.1 Ratios
A ratio is a numerical representation of the relationship between two parts of a whole or of the relationship of one part to the whole. Ratios may be written with a colon (:) between the numbers, which may be read as per, of, to, or in. The ratio 1:2 could mean that the second part has twice the value (e.g., size, number, weight, volume) of the first part, or the ratio could indicate that one part is something within a total of two parts. Ratios may also be written as fractions, and it is the ratio in fraction form that is commonly used in pharmacy calculations.
 Math Morsel
Math Morsel
A ratio written in the form of a fraction is commonly used in pharmacy calculations.
1:2 |
is read as |
1 part to 2 parts |
and may also be written as |
3:4 |
is read as |
3 parts to 4 parts |
and may also be written as |
1:20 |
is read as |
1 part to 20 parts |
and may also be written as |
1:10 |
is read as |
1 part to 10 parts |
and may also be written as |
A ratio can be any numerical relation you need to show. With medications, you commonly use a ratio to express the weight or strength of a drug per dose or volumetric measurement. Ratios are commonly used to express concentrations of a medication in solution. For example, a 1:100 concentration of a medication means that there is 1 part of the medication in 100 parts of the solution (1 g per 100 mL). It is also common to reverse the order of the values written in a ratio.
 Math Morsel
Math Morsel
Ratios of drugs are usually written as the concentration of a drug per dose or the weight of a drug in a unit of measurement.
250 mg:1 tablet |
or |
1 tablet:250 mg |
1 g:100 mL |
or |
100 mL:1 g |
500 mg:20 mL |
or |
20 mL:500 mg |
A ratio may be manipulated by multiplying or dividing both parts of the ratio by the same factor. Pharmacists and pharmacy technicians use this process when calculating the volume of a medication to be administered or, in some cases, the amount of a drug per volume of the medication administered.
Ampules are single-dose containers of medication that are opened at the time of use.
Some medication labels, especially those of injectable medications, have more than one ratio listed. For example, the aminophylline label (see Figure 2.1) includes three ratios, each descriptive of the medication’s concentration. The first ratio, shown within the green bar of the medication label, is 500 mg/20 mL and represents the total amount of medication in the entire ampule. The second ratio on the medication label is 25 mg/mL and represents the amount of medication in 1 mL. The third ratio is 19.7 mg/mL and describes the concentration of the medication in its anhydrous-theophylline state. The pharmacist may use this concentration to further analyze the dosage. The ratio indicating the total amount of medication in the ampule is of the most importance to a pharmacy technician. Typically, this ratio is the most prominent one on the label, as is the case for this label.
Figure 2.1 Ratios on an Ampule Label
When more than one ratio appears on a medication label, the most prominent ratio—in this case, 500 mg/20 mL—is typically the most important.

Medication labels indicate the ratio of the active ingredient, and, as described in Chapter 1, the ratio may be manipulated by multiplying or dividing both parts of the ratio by the same factor. If the dose needs to be increased, you multiply the ratio by a factor. If the dose needs to be decreased, you divide the ratio by a factor.
Example 2.1.1
Using the label shown in Figure 2.1, how many milligrams of aminophylline were ordered if two ampules were administered and each ampule contained 500 mg/20 mL?
For two ampules, you multiply both parts of the ratio by 2.
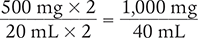
Answer: The order was for 1,000 mg of aminophylline.
Example 2.1.2

Using the label shown in Figure 2.1, how many milligrams of aminophylline were ordered if half of an ampule was administered and each ampule contained 500 mg/20 mL?
To determine the number of milligrams in half of an ampule, you can either divide both parts of the ratio by 2 or multiply both parts of the ratio by ½
Division Method
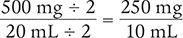
Multiplication Method
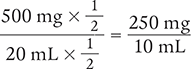
Answer: The order was for 250 mg of aminophylline.
 Pharm Fact
Pharm Fact
Pharmacy technicians should be aware that some drug manufacturers always capitalize the name of the drug on a medication label, regardless of whether the medication is a generic product or a brand name. For that reason, they should be sure to memorize both the generic and brand names of drugs.
Example 2.1.3
A physician has ordered that a patient take ½ of a 137 microgram (mcg) tablet of levothyroxine. How many micrograms will the patient take?

This label does not overtly indicate the ratio. However, you can determine a ratio because the label says each tablet contains 137 mcg of levothyroxine. Therefore, the ratio is 137 mcg/1 tablet. You can use either multiplication or division to solve the problem. You can also use the dimensional analysis method you learned in Chapter 1.
Multiplication Method
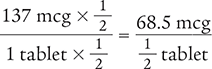
Division Method
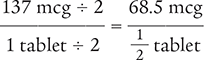
Dimensional Analysis Method
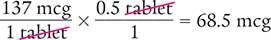
Answer: The patient will take ½ tablet of levothyroxine, which contains 68.5 mcg.
Some medications are ordered in concentrations that are expressed as a ratio. Typically, these medications are available in a very small percentage (less than 1%). The dosage form influences the ratio. A common dosage form is a solution (a liquid mixture in which the minor component, the solute, is uniformly distributed within the major component, the solvent). A similar dosage form is a suspension, or a mixture in which solute particles are mixed with, but not dissolved in, a fluid. The following examples use a 1:10,000 ratio.
1 g active ingredient:10,000 g of a solid, such as a cream
1 g active ingredient:10,000 mL of a solution
1 mL active ingredient:10,000 mL of a liquid
Example 2.1.4
A 1:100 solution has 1 g active ingredient in 100 mL. How much active ingredient is present in 300 mL of this solution?
You can either set up a ratio to solve this problem, or you can use the dimensional analysis method.
Ratio Method
To begin, set up a ratio to solve for the unknown variable x. In this problem, x represents the active ingredient.
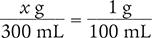
Because these fractions are equivalent, you can cross multiply and the equations will still equal one another.
x g (100 mL) = 300 mL (1 g)
Then solve for x by dividing each side of the equation by 100 mL and canceling the similar units (like units) in the numerators and in the denominators.
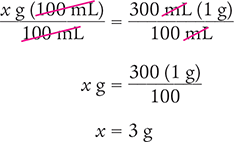
Dimensional Analysis Method
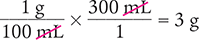
Answer: There are 3 g of active ingredient in 300 mL of solution.
2.1 Problem Set
Express the following ratios as fractions and then reduce the fractions to their lowest terms.
3:7
8:6
3:4
4:6
1:7
Reduce the following fractions to their lowest terms and then express these fractions as ratios.
Applications
State the ratio for the following doses.
30 mg capsule of Cymbalta

100 mg capsule of Dilantin

5 mL dose of oral suspension containing 250 mg of amoxicillin

Use the ratios calculated in items 11–13 to calculate the amount of medication in the following doses. Write your answers as ratios.
3 capsules of Cymbalta
2 capsules of Dilantin
15 mL of amoxicillin suspension
Fill in the blanks.
A 10:1,000 solution contains __________ g of active ingredient in __________ mL of product, and 100 mL of that solution contains __________ g.
A 1:100 solution contains __________ g of active ingredient in __________ mL of product, and 500 mL of that solution contains __________ g.
A 1:250 solution contains __________ g of active ingredient in __________ mL of product, and 1,000 mL of that solution contains __________ g.
A 1:1,000 solution contains __________ g of active ingredient in __________ mL of product, and 50 mL of that solution contains __________ g.
Self-check your work in Appendix A.